Robust Gesture Recognition and Classification for Visually Impaired Persons Using Growth Optimizer with Deep Stacked Autoencoder

Abstract

Visual impairment affects the major population of the world, and impaired vision people need assistance for their day-to-day activities. With the enormous growth and usage of new technologies, various devices were developed to help them with object identification in addition to navigation in the indoor and outdoor surroundings. Gesture detection and classification for blind people aims to develop technologies to assist those people to navigate their surroundings more easily. To achieve this goal, using machine learning and computer vision techniques is a better solution to classify and detect hand gestures. Such methods are utilized for finding the shape, position, and movement of the hands in real-time. With this motivation, this article presents a robust gesture recognition and classification using growth optimizer with deep stacked autoencoder (RGRC-GODSAE) model for visually impaired persons. The goal of the RGRC-GODSAE technique lies in the accurate recognition and classification of gestures to assist visually impaired persons. The RGRC-GODSAE technique follows the Gabor filter approach at the initial stage to remove noise. In addition, the RGRC-GODSAE technique uses the ShuffleNet model as a feature extractor and the GO algorithm as a hyperparameter optimizer. Finally, the deep stacked autoencoder model is exploited for the automated recognition and classification of gestures. The experimental validation of the RGRC-GODSAE technique is carried out on the benchmark dataset. The extensive comparison study showed better gesture recognition performance of the RGRC-GODSAE technique over other deep learning models.

Main article text

INTRODUCTION

Currently, blind and visually impaired persons are switching from standard writing and reading in Braille to using computers with user-friendly applications ( Montazerin et al., 2022). Hand gestures have an eminent role in assistive technology for individuals with low vision, where a good user interaction model is of great significance. Certain applications and devices in this domain can significantly benefit from an intuitive, agile, and natural communication system that uses hand gestures ( Xu et al., 2023). In the computer vision (CV) domain, gesture language recognition has gained special attention to precisely detect gesture movement and understand the sense of gesture language for machines or communicators. The detection of gesture language action has enormous application in robot perception, enhancing people with speech impairments and improvising nonverbal data transfer ( Rashid et al., 2022). As gesture language movement is usually very fast, the usage of conventional frame cameras presents greater difficulties, such as computational complexity and blur and overlap ( Shokat et al., 2021). Gesture customization is significant for the many motor-impaired persons with heavy movement limitations who are unable to do some gestures described by the manufacturer of the system. In that mechanism, the small training set made individually for all users would allow the system to be fully utilized ( Jyothsna et al., 2022). The small training set in the gesture recognition approach was previously inspected, for example, for the spiking neural network (NN) method and hand gesture recognition (HGR) with a deep sensor concept.

Machine vision-related gesture recognition does not need physical interference of the user nor the use of specialized equipment or additional sensors ( Shen et al., 2023). Rather, it should be trained with loads of image datasets for gaining a highly precise recognition method and attain precise HGR ( Padmavathi, 2021). Previous gesture detection approaches are based on the manual extraction of gesture features (e.g., texture, shape, and color) for gesture detection, but these techniques depend on the knowledge of experts and cannot resolve the issue of complicated images with skin-like backgrounds ( De Fazio et al., 2022). With the progress of deep learning (DL) methods, numerous researchers have used advanced DL approaches for gesture detection. Comparatively, using DL approaches for gesture detection has features of high accuracy, self-extraction of features, greater efficiency, and strong adaptability and robustness for managing more data ( Muneeb et al., 2023). DL methods such as convolution neural networks (CNN) and long short-term memory (LSTM) are better choices for classifying and detecting a sequence of gestures. However, the methods operate under the assumption that the start and end places of the gesture series are available before all individual gestures are detected ( Hegde et al., 2022).

This article presents a robust gesture recognition and classification using growth optimizer with deep stacked autoencoder (RGRC-GODSAE) model for visually impaired persons. The goal of the RGRC-GODSAE technique lies in the accurate recognition and classification of gestures to assist visually impaired persons. The RGRC-GODSAE technique follows the Gabor filter (GF) approach at the initial stage to remove noise. In addition, the RGRC-GODSAE technique uses the ShuffleNet model as a feature extractor and the GO algorithm as a hyperparameter optimizer. Finally, the deep stacked autoencoder (DSAE) model is exploited for the automated recognition and classification of gestures. The experimental validation of the RGRC-GODSAE technique is carried out on the benchmark dataset.

LITERATURE REVIEW

Gaidhani et al. (2022) introduced a CNN method, as it has more precision compared with other techniques. Python is a computer program written in the programming language that can be utilized for model training, depending on the CNN mechanism. Using Indian sign language, the input with a preexisting dataset created is compared so that the method can understand hand gestures. Users could detect the signs presented by transforming sign language into the text as outputs by sign language interpreters. Miah et al. (2023) modeled a multistage spatial attention-related NN for HGC to solve the difficulties. This method has phases; the author implemented a spatial attention module and feature extractors utilizing self-attention from the original data. Later, the author explored attributes connected with the original data to gain modality feature embedding. Likewise, the author made an attention map and feature vector in the second phase with the self-attention technique and feature extraction architecture. Raja et al. (2019) indicated the implementation and model of a facial detection system for blind people with image processing. The developed device has programmed raspberry pi hardware. The data are given to the device in the image format. The imageries captured are preprocessed in the raspberry pi module utilizing the k-nearest neighbor (KNN) approach, the face is detected, and the name is given into text-to-speech conversion modules.

Hegde et al. (2021) presented a user-friendly, low-cost, portable, low-power, robust, and reliable solution for smooth navigation. This study is mainly for blind persons. It has an in-built sensor that spreads ultrasonic waves in an individual’s direction by scanning 5-6 m of range. As soon as the obstacle can be identified, the sensor finds it and transfers it to the device that generated an automatic voice in the earphone linked to one’s ear. Yoo et al. (2022) modeled a hybrid HGR that integrates a vision-based gesture system and an inertial measurement unit (IMU)-related motion capture mechanism. First, vision-related commands and IMU-based commands are classified as drone operation commands. Second, IMU-related control command is mapped intuitively to enable the drone to go in a similar direction through predicted orientation sensed by thumb-mounted micro-IMU. In Subburaj et al. (2023), human gestures are classified utilizing data gathered from curved piezoelectric sensors, which include coughing, elbow movement, wrist bending, neck bending, and wrist turning. Machine learning (ML) methods enabled with K-mer are optimized and developed for performing HGR from the obtained data. Three ML methods, namely, k-NN, SVM, and RF, are analyzed and executed with K-mer.

Chen et al. (2021) modeled a wearable navigation gadget for blind people by compiling the semantic visual of the powerful mobile computing environment and SLAM (Simultaneous Localization and Mapping). The author concentrated on the integration of SLAM technology with the abstraction of semantic data from the atmosphere. In Zakariah et al. (2022), they devised a system that would utilize the visual hand data depending on Arabic Sign Language and combined this visual dataset with text data. Different data augmentation and preprocessing methods were implemented in the images. The experiments were conducted with different pretrained methods on the given data. The EfficientNetB4 method was the better best fit for the case.

MATERIALS AND METHODS

In this article, we have introduced a new RGRC-GODSAE technique for effectual recognition and classification of gestures to aid visually impaired persons. Figure 1 demonstrates the workflow of the RGRC-GODSAE system. The main aim of the RGRC-GODSAE technique lies in the accurate recognition and classification of gestures to assist visually impaired persons. The RGRC-GODSAE technique comprises several subprocesses, namely, GF-based noise elimination, ShuffleNet feature extractor, GO-based hyperparameter tuning, and DSAE-based gesture recognition.

Figure 1:

Workflow of RGRC-GODSAE system. RGRC-GODSAE, robust gesture recognition and classification using growth optimizer with deep stacked autoencoder.

Noise elimination using GF approach

To eliminate noise, the GF approach is used. In image processing, the GF method is broadly used to analyze image orientation and texture ( Lee et al., 2023). It depends on a family of bandpass filters called the GF method that can be utilized for abstracting attributes from images through the convolution of the image with a group of GF methods of various frequencies and orientations. It refers to a complex sinusoidal wave, and a Gaussian function modulates it. It can be defined in the frequency and spatial domains, which allows it to inspect an image in both domains concurrently. The two parameters of the filter are altered to control its orientation and frequency.

ShuffleNet feature extractor

For effectual derivation of the feature vectors, the ShuffleNet model is used. Among MobileNetV2, ShuffleNetV1, and Xception, ShuffleNetV2 has the fastest speed and the highest accuracy ( Fu et al., 2023). It primarily exploits two new operations, channel shuffle and pointwise group convolution, that considerably lessen the computational cost without affecting detection performance. Group convolution (GC) was initially applied in AlexNet to distribute the network through two graphics processing units (GPUs), which showed its efficiency in ResNeXt. The conventional convolution (CC) adopts a channel-dense connection that implements a convolution function on all the channels of the input feature. For CC, the height and width of the kernels are K, and C signifies the number of input channels; when the amount of the kernel denotes N, then the amount of output channels is also N:

(1) $$P\mathrm{(}CC\mathrm{)}=\hspace{0.17em}K\hspace{0.17em}\times \hspace{0.17em}K\hspace{0.17em}\times \hspace{0.17em}C\hspace{0.17em}\times \hspace{0.17em}N\hspace{0.17em}\mathrm{(}parameters\mathrm{)}$$

For GC, the channel of input features was separated into G groups so that the amount of kernel can be C/G; the outcomes from the G group were concatenated into large feature output of the N channels:

(2) $$P\mathrm{(}GC\mathrm{)}=\hspace{0.17em}K\hspace{0.17em}\times \hspace{0.17em}K\hspace{0.17em}\times \frac{C}{G}\times \hspace{0.17em}N\hspace{0.17em}\mathrm{(}parameters\mathrm{)}$$

From the aforementioned formula, we could say that the amount of parameters in GC is much smaller than in CC. However, GC causes the issue that dissimilar groups might no longer share data. Thus, ShuffleNet implements a channel shuffle process on the output feature, so that data can be circulated over various groups without increasing the computational cost. In ShuffleNetV2 unit 1, a channel split can be initially executed on the input feature map that can be evenly divided into dual branches. The right branch undergoes three convolutional functions, while the left branch remains the same. Both branches are concatenated to fuse the features once the convolution is finished. In conclusion, Channel Shuffle transmits data between various groups. In ShuffleNetsV2 unit 2, the channel was not separated in the early stages, and the feature map can be inputted directly toward both branches. These two branches exploit 3 × 3 deep convolutional layers for minimizing the dimension of the feature map. Later, the concatenation function can be implemented on the output of both branches.

Hyperparameter tuning using GO algorithm

In this work, the GO algorithm is utilized for optimal hyperparameter selection of the ShuffleNet model. GO algorithm assumes that persons train and reflect as it is developed in society ( Fatani et al., 2023). During the learning model, the data have been gathered in the environment, but the reflection purpose for examining the limitations enhance the learning process.

Generally, the GO begins with utilizing Eq. (3) for generating the population X that represents the solutions for the testing problem:

(3) $$X_i=r\times \mathrm{(}U-L\mathrm{)}+L,\hspace{0.17em}i=1,\dots ,N$$

whereas r refers to the arbitrary value and the restrictions of searching the area of the problems can be signified utilizing U and L. N denotes the entire count of solutions in X. Later, X can be separated into three parts based on the parameters called P ₁ = 5. A primary part includes leaders and elites (different in 2 to P ₁). The second part has the middle level (i.e., from P ₁+1 to N− P ₁), and the tertiary part comprises the bottom level (i.e., N− P ₁+1 and N), but an optimum solution was the leader of the upper level.

By challenging the disparities among people, inspecting the reasons for individual differences, and learning based on them, individuals are significantly assisted in their development. The learning stage of GO mimics four key gaps, which can be in the form:

(4) $$\begin{array}{l}{G}_1=X_b-X_{bt}\\ G_2=X_b-X_w\\ G_1=X_{bt}-X_w\\ G_1=X_{r1}-X_{r2}\end{array}$$

in which, X _b, X _bt , and X _w are simply the best, better, and worse solutions, correspondingly; besides, X _{r 1} and X _{r 2} denote two arbitrary solutions. G _k( k = 1, 2, 3, 4) signifies the gap utilized for improving skills learned and reducing the variance among them. Besides, to reflect the difference among groups, the parameter termed as a learning factor (LF) was executed, and its formula can be provided as:

(5) $$L{F}_k=\frac{\left|\left|G_k\right|\right|}{{\Sigma }_{k=1}^4\left|\left|G_k\right|\right|},k=1,2,3,4$$

Next, the individual considers his learning skill utilizing the parameter ( SF _i ):

(6) $$S{F}_i=\frac{G{R}_i}{G{R}_{\text{max\hspace{0.17em}}}}\hspace{0.17em}$$

whereas GR _max and GR _i indicate the maximal growth resistance of X and the development of X _i correspondingly.

Based on the data gathered in LF _k and SF _i , every X _i is to obtain novel knowledge in the solution appropriate to all the gaps in G _k utilizing the knowledge acquisition ( KA) that can be determined as:

(7) $$K{A}_k=S{F}_i\times L{F}_k\times G_k,\hspace{0.17em}k=1,2,3,4\hspace{0.17em}$$

Then, the solution X _i enhanced their data utilizing the following equation:

(8) $$X_i\mathrm{(}t+1\mathrm{)}=X_i\mathrm{(}t\mathrm{)}+{\displaystyle \sum _{k=1}^{4}K{A}_k}$$

The quality of the upgrade form of X _i was calculated and related to the preceding one to define if there is a major difference between them:

(9) $$\begin{array}{l}{X}_i\mathrm{(}t+1\mathrm{)}=\hspace{0.17em}\\ \{\begin{array}{cc}{X}_i\mathrm{(}t+1\mathrm{)}\hspace{0.17em}& iff\mathrm{(}{X}_i\mathrm{(}t+1\mathrm{)}\mathrm{)}\le f\mathrm{(}X\mathrm{(}t\mathrm{)}\mathrm{)}\\ \{\begin{array}{c}{X}_i\mathrm{(}t+1\mathrm{)}\hspace{0.17em}if\hspace{0.17em}{r}_1<P_{2\text{'}}ind\mathrm{(}i\mathrm{)}=ind\mathrm{(}1\mathrm{)}\\ X_i\mathrm{(}t\mathrm{)}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}otherwise\end{array}& otherwise\end{array}\hspace{0.17em}\end{array}$$

in which r ₂ denotes the arbitrary number, and P ₂ = 0.001 signifies the probability of retention. ind( i) represents the ranking of X _i dependent upon ascending order X utilizing the fitness value.

The solution can progress its capability to reflect on the data that can be learned, representing that X can recognize their entire region of weakness and maintain their data. It must implement the unwanted elements of a successful X, but recollects its outstanding qualities. Once the lesson of a particular feature cannot be fixed, the previous data can be unrestricted and systematic learning must restart. Equations (10) and (11) are employed for mathematical formulas during this procedure:

(10) $$X_j\mathrm{(}t+1\mathrm{)}=\{\begin{array}{c}\{\begin{array}{c}{r}_4\times \mathrm{(}U-L\mathrm{)}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}if\hspace{0.17em}{r}_3<AF\\ X_i\mathrm{(}t\mathrm{)}+r_5\times \mathrm{(}{X}_R-X_j\mathrm{(}t\mathrm{)}\mathrm{)}\hspace{0.17em}otherwise\end{array}\hspace{0.17em}otherwise\\ X_i\mathrm{(}t\mathrm{)}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}otherwise\end{array},\hspace{0.17em}$$

(11) $$AF=0.01+0.99\times \left(1-\frac{FEs}{{\text{max}}_{FE}}\right)\hspace{0.17em}$$

whereas r ₃, r ₄, and r ₅ represent the random values; X _R denotes the solution determined as the top P ₁+1 results in X; and AP implies the attenuation aspect dependent on function estimation PE and entire count of functions estimations max. Later the whole reflection phase, X _{j ,} can estimate its growth related to the learning stage. Thus, Eq. (9) is also executed for achieving this task.

The GO method makes extraction of a fitness function (FF) to get better classification performance. It ascertains a positive integer that specifies the candidate solution’s better performance. Here the minimal classifier error rate is the FF, as given in Eq. (12):

(12) $$\begin{array}{c}Fitness\mathrm{(}{x}_i\mathrm{)}=ClassifierErrorRate\mathrm{(}{x}_i\mathrm{)}\\ =\frac{number\hspace{0.17em}of\hspace{0.17em}misclassified\hspace{0.17em}samples}{Total\hspace{0.17em}number\hspace{0.17em}of\hspace{0.17em}samples}*100\hspace{0.17em}\end{array}$$

Gesture classification using DSAE model

At the final stage, the DSAE model is exploited for accurate detection and classification of gestures. AE is a DNN used for learning a compressed representation of an input dataset ( Samee et al., 2022). The AE was trained to remove irrelevant noise, and data and its output were an encoding form for the sequence of data. The AE includes encoder and decoder models. The encoder maps the input variable into compressed format, whereas the decoder tries to reverse the mapping for regenerating input. Using the scaled conjugate gradient algorithm, SAE was trained in an unsupervised way in this study, with 1000 training epochs. The AE is used for ignoring the irrelevant ones and extracting the hidden features. The input variable was fed into the AE and the neurons in the hidden layer were attuned to be lesser than the input size. By including a regularization for the activation of neurons to the cost function we combined sparsity in the AE. The cost function was the MSE function altered to have two terms as shown in Eq. (13): the sparsity regularization, Ω-sparsity, and the weight regularization, Ω-weights. The weight regularization term avoids the value of neuron weight from increasing, which accordingly minimizes the sparsity regularizer. The sparsity regularizer restricts the outputs from the neuron to be lower, which allows the AE to determine representations from a smaller part of the training sample. Equations (14) and (15) illustrated the mathematical representation of Ω-sparsity and Ω-weights, correspondingly:

(13) $$\begin{array}{c}E=\underset{mean\hspace{0.17em}squared\hspace{0.17em}error}{\underbrace{\frac{1}{M}{\displaystyle \sum _{n=1}^M{{\displaystyle \sum _{k=1}^N\mathrm{(}{x}_{kn}-X_{kn}\mathrm{)}}}^2}}}\\ +\lambda \times {\Omega }_{weights}\\ +\beta \times {\Omega }_{sparsiiy}\end{array}$$

where N indicates the number of input parameters in the training dataset, M denotes the number of instances in the training set, X represents the estimate of the training instance, x denotes a training sample, and β indicates coefficients of the weight regularizer and sparsity, correspondingly:

(14) $${\Omega }_{weighis}=\frac{1}{M}{\displaystyle \sum _l^L{\displaystyle \sum _j^M{\displaystyle \sum _i^k{\mathrm{(}{w}_{ji}^{\mathrm{(}l\mathrm{)}}\mathrm{)}}^2}}}$$

where w denotes the weight matrix and L signifies the size of hidden layers:

(15) $$\begin{array}{c}{\Omega }_{sparsiiy}={\displaystyle \sum _{i=1}^{D^{\mathrm{(}1\mathrm{)}}}KL\mathrm{(}\rho \left|\right|{\widehat{\rho }}_i\mathrm{)}}\\ ={\displaystyle \sum _{i=1}^{D^{\mathrm{(}1\mathrm{)}}}\rho log}\mathrm{(}\frac{\rho }{{\widehat{\rho }}_i}\mathrm{)}\hspace{0.17em}\\ +\mathrm{(}1-\rho \mathrm{)}log\mathrm{(}\frac{1-\rho }{1-{\widehat{\rho }}_i}\mathrm{)}\end{array}$$

(16) $$f\mathrm{(}z\mathrm{)}=\{\begin{array}{l}0,ifz\le 0\hfill \\ z,if0<z<1\hfill \\ 1,ifz\ge 1\hfill \end{array}\hspace{0.17em}$$

where KL signifies the Kullback–Leibler divergence value between ρ _j and $${\widehat{\rho }}_i.{\widehat{\rho }}_i$$ signifies the average activation of neuron i, and ρ characterizes the desired activation. Figure 2 represents the infrastructure of the SAE method.

Figure 2:

Infrastructure of SAE. Abbreviation: SAE, stacked autoencoder.

We have applied an SAE, in two phases, by training the initial AE, AE-1, on the input variable, and utilizing the feature abstracted from AE-1 as inputted to the next phase, AE-2. The transfer function utilized for the initial encoder (Encoder−1) was the positive saturating linear transfer, whereas the ordinary linear transfer function can be utilized for the initial decoder (Decoder−1). Positive saturating linear was applied in encoder and decoder models as shown in Eq. (16). In this work, each input variable, M = 36, N = 540, was fed into AE-1. The amount of features derived from stage 1 was 10 features, hence the amount of inputs to AE-2 was = 10, N = 540. Five relevant features are extracted from AE-2 and applied in the prediction stage. We have implemented a lot of research to set the value of the learning parameter and the recorded value was the one that produced the minimal root mean squared error (RMSE) for the anticipated value of the response variable.

RESULTS AND DISCUSSION

In this section, the experimental validation of the RGRC-GODSAE method can be examined on the dataset, comprising several classes, namely, Wrist watch (Cl-1), Dog (Cl-2), Stop sign (Cl-3), Person (Cl-4), Stairs (Cl-5), Chair (Cl-6), Table (Cl-7), and Washroom (Cl-8). The dataset shows 1600 samples with 8 classes, as shown in Table 1. For experimental validation, 80:20 and 70:30 of training/testing dataset is used.

Table 1:

Details of database.

Class	Labels	No. of samples
Wrist watch	Cl-1	200
Dog	Cl-2	200
Stop sign	Cl-3	200
Person	Cl-4	200
Stairs	Cl-5	200
Chair	Cl-6	200
Table	Cl-7	200
Washroom	Cl-8	200
Total number of samples		1600

In Figure 3, the confusion matrices of the RGRC-GODSAE method are examined in detail. The results indicate that the RGRC-GODSAE technique recognizes eight different class labels.

Figure 3:

Confusion matrices of RGRC-GODSAE approach (a, b) 80:20 of TRP/TSP and (c, d) 70:30 of TRP/TSP. RGRC-GODSAE, robust gesture recognition and classification using growth optimizer with deep stacked autoencoder.

In Table 2 and Figure 4, the gesture recognition outcomes of the RGRC-GODSAE method under 80:20 of TRP/TSP are reported. The experimental values recognized that the RGRC-GODSAE technique accurately detects all the classes. For instance, on 80% of TRP, the RGRC-GODSAE technique attains an average accu _y of 99.77%, prec _n of 99.08%, recall of 99.06%, F _score of 99.07%, and G _measure of 99.07%. Additionally, on 20% of TSP, the RGRC-GODSAE approach attains average accu _y of 99.61%, prec _n of 98.50%, recall of 98.56%, F _score of 98.50%, and G _measure of 98.52%.

Table 2:

Gesture recognition outcome of RGRC-GODSAE approach on 80:20 of TRP/TSP.

Class	Accuracy	Precision	Recall	F-Score	G-Measure
Training phase (80%)
Wrist watch (Cl-1)	99.84	98.84	100.00	99.42	99.42
Dog (Cl-2)	99.69	99.36	98.11	98.73	98.74
Stop sign (Cl-3)	99.53	98.14	98.14	98.14	98.14
Person (Cl-4)	100.00	100.00	100.00	100.00	100.00
Stairs (Cl-5)	99.92	99.38	100.00	99.69	99.69
Chair (Cl-6)	99.53	97.53	98.75	98.14	98.14
Table (Cl-7)	99.92	100.00	99.37	99.68	99.68
Washroom (Cl-8)	99.69	99.36	98.11	98.73	98.74
Average	99.77	99.08	99.06	99.07	99.07
Testing phase (20%)
Wrist watch (Cl-1)	100.00	100.00	100.00	100.00	100.00
Dog (Cl-2)	100.00	100.00	100.00	100.00	100.00
Stop sign (Cl-3)	99.69	97.50	100.00	98.73	98.74
Person (Cl-4)	99.38	100.00	95.65	97.78	97.80
Stairs (Cl-5)	99.69	97.62	100.00	98.80	98.80
Chair (Cl-6)	99.69	97.56	100.00	98.77	98.77
Table (Cl-7)	99.06	100.00	92.86	96.30	96.36
Washroom (Cl-8)	99.38	95.35	100.00	97.62	97.65
Average	99.61	98.50	98.56	98.50	98.52

Figure 4:

Average outcome of RGRC-GODSAE approach on 80:20 of TRP/TSP.

Figure 5 inspects the accuracy of the RGRC-GODSAE method in the training and validation on 80:20 of TRP/TSP. The result specified that the RGRC-GODSAE technique has greater accuracy values over higher epochs. Also, the greater validation accuracy over training accuracy shows that the RGRC-GODSAE method learns productively on 80:20 of TRP/TSP.

Figure 5:

Accuracy curve of RGRC-GODSAE approach on 80:20 of TRP/TSP. Abbreviation: RGRC-GODSAE, robust gesture recognition and classification using growth optimizer with deep stacked autoencoder.

The loss analysis of the RGRC-GODSAE method in training and validation is given on 80:20 of TRP/TSP in Figure 6. The result indicates that the RGRC-GODSAE approach reaches a closer value of training and validation loss. The RGRC-GODSAE method learns productively on 80:20 of TRP/TSP.

Figure 6:

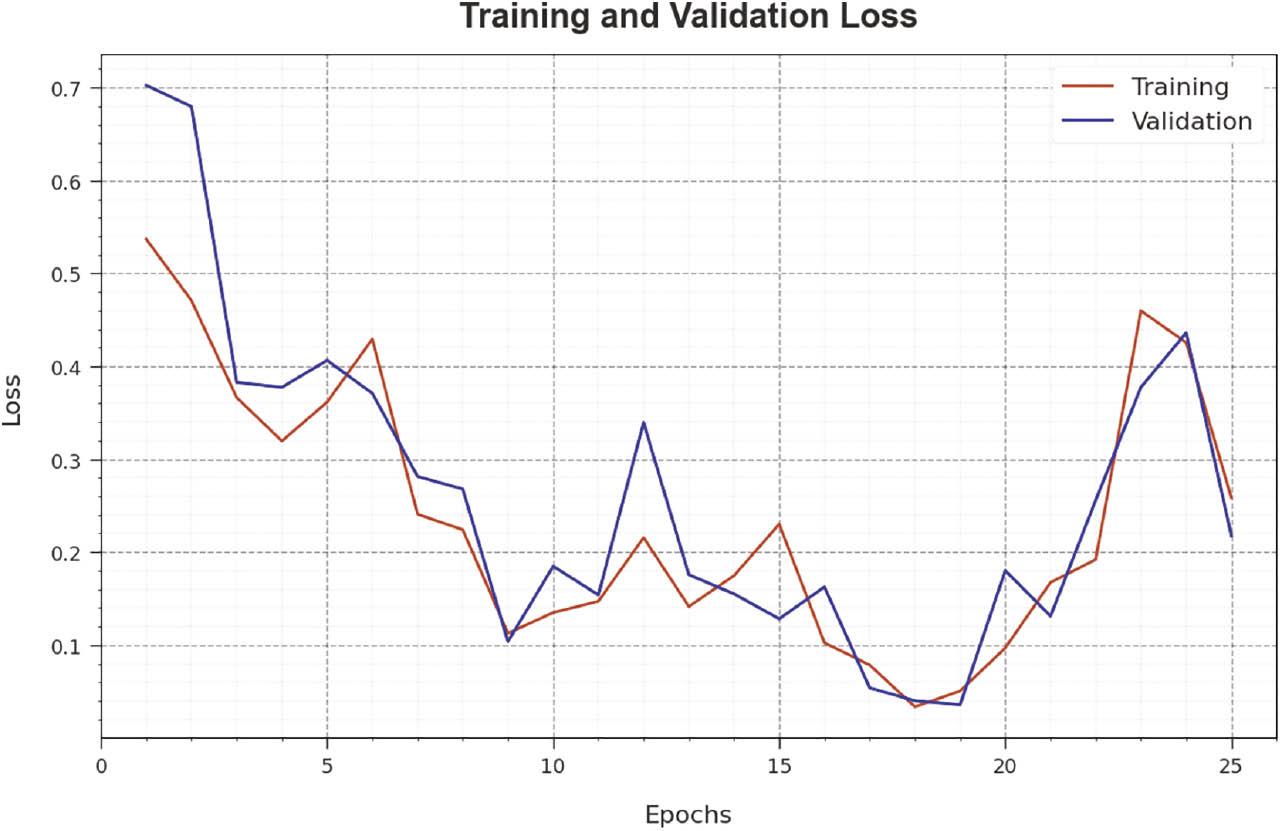
Loss curve of RGRC-GODSAE approach on 80:20 of TRP/TSP. Abbreviation: RGRC-GODSAE, robust gesture recognition and classification using growth optimizer with deep stacked autoencoder.

The detailed precision–recall (PR) curve of the RGRC-GODSAE technique is demonstrated on 80:20 of TRP/TSP in Figure 7. The figure states that the RGRC-GODSAE approach has increasing values of PR. Furthermore, the RGRC-GODSAE technique can reach higher PR values in all classes.

Figure 7:

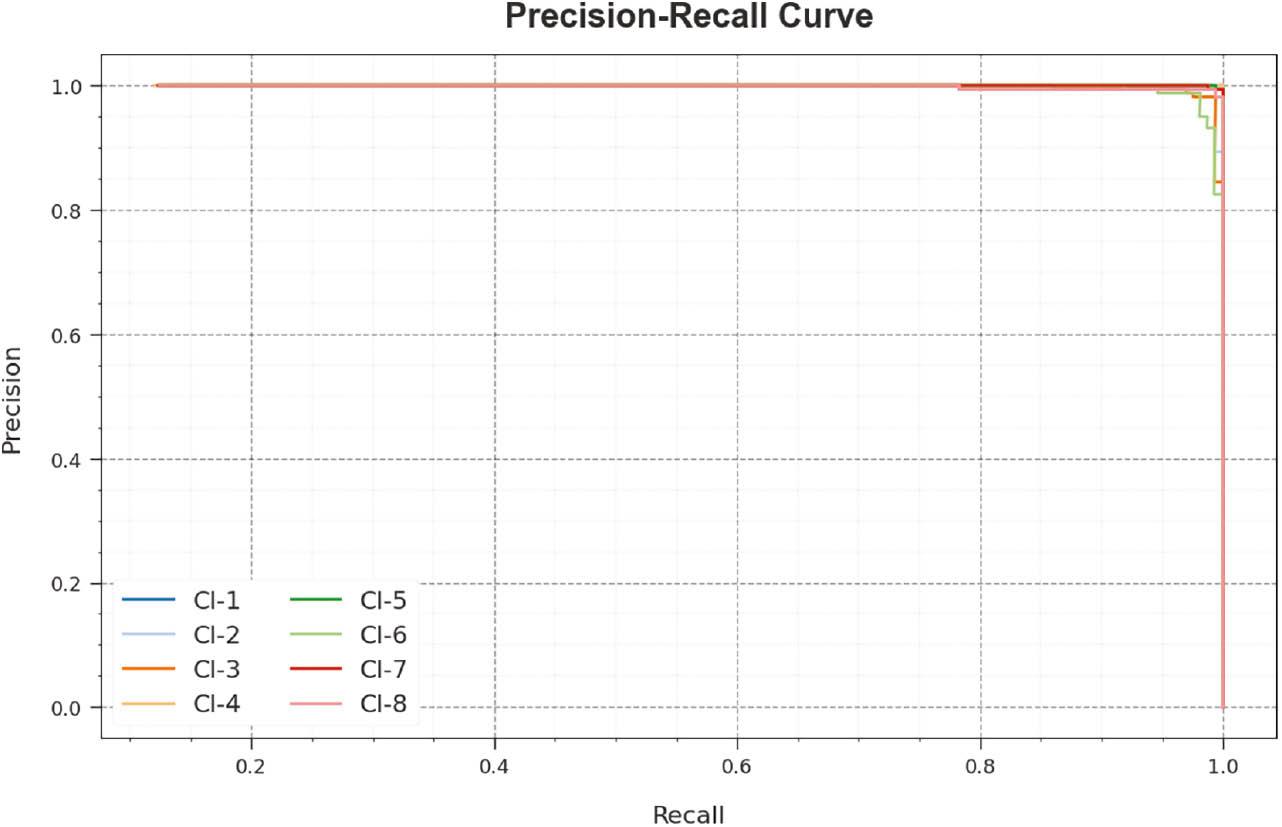
PR curve of RGRC-GODSAE approach on 80:20 of TRP/TSP. Abbreviations: PR, precision–recall; RGRC-GODSAE, robust gesture recognition and classification using growth optimizer with deep stacked autoencoder.

In Figure 8, a receiver operating characteristic (ROC) study of the RGRC-GODSAE technique is revealed on 80:20 of TRP/TSP. The figure describes that the RGRC-GODSAE method resulted in better ROC values. Besides, the RGRC-GODSAE technique can extend enhanced ROC values on all classes.

Figure 8:

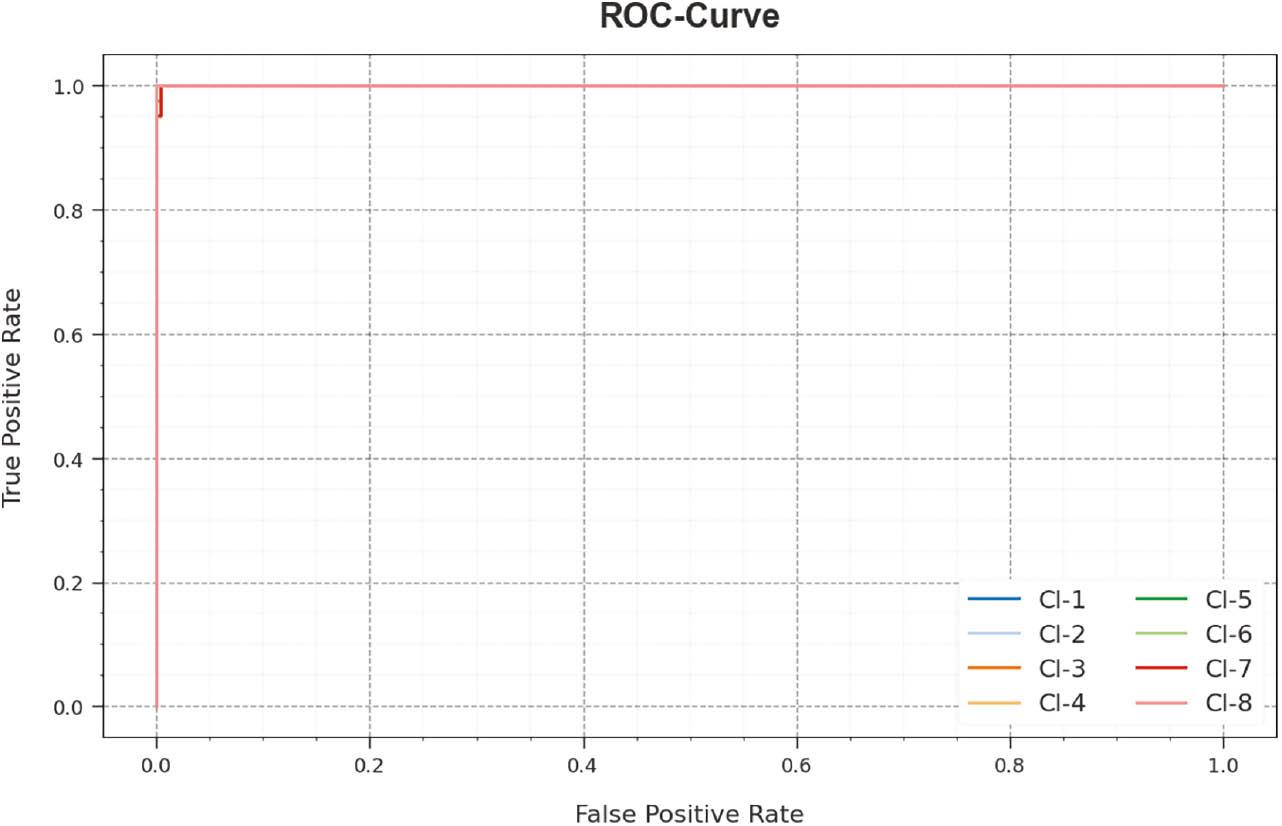
ROC curve of RGRC-GODSAE approach on 80:20 of TRP/TSP. Abbreviations: RGRC-GODSAE, robust gesture recognition and classification using growth optimizer with deep stacked autoencoder; ROC, receiver operating characteristic.

In Table 3 and Figure 9, the gesture recognition outcomes of the RGRC-GODSAE method under 70:30 of TRP/TSP are reported. The experimental values recognize that the RGRC-GODSAE technique accurately detects all the classes. For example, on 70% of TRP, the RGRC-GODSAE method attains an average accu _y of 98.48%, prec _n of 93.89%, recall of 93.95%, F _score of 93.91%, and G _measure of 93.92%. In addition, on 30% of TSP, the RGRC-GODSAE technique attains an average accu _y of 98.54%, prec _n of 94.42%, recall of 94.17%, F _score of 94.26%, and G _measure of 94.28%.

Table 3:

Gesture recognition outcome of RGRC-GODSAE approach on 70:30 of TRP/TSP.

Class	Accuracy	Precision	Recall	F-Score	G-Measure
Training phase (70%)
Wrist watch (Cl-1)	98.39	92.48	93.89	93.18	93.18
Dog (Cl-2)	98.57	92.81	95.56	94.16	94.17
Stop sign (Cl-3)	98.66	95.04	94.37	94.70	94.70
Person (Cl-4)	98.75	94.29	95.65	94.96	94.97
Stairs (Cl-5)	98.04	91.30	92.65	91.97	91.97
Chair (Cl-6)	98.66	97.28	92.86	95.02	95.04
Table (Cl-7)	98.39	92.86	94.20	93.53	93.53
Washroom (Cl-8)	98.39	95.07	92.47	93.75	93.76
Average	98.48	93.89	93.95	93.91	93.92
Testing phase (30%)
Wrist watch (Cl-1)	97.92	91.55	94.20	92.86	92.87
Dog (Cl-2)	98.96	96.88	95.38	96.12	96.13
Stop sign (Cl-3)	98.33	90.32	96.55	93.33	93.39
Person (Cl-4)	98.75	93.75	96.77	95.24	95.25
Stairs (Cl-5)	97.50	90.62	90.62	90.62	90.62
Chair (Cl-6)	99.17	97.73	93.48	95.56	95.58
Table (Cl-7)	98.75	98.28	91.94	95.00	95.05
Washroom (Cl-8)	98.96	96.23	94.44	95.33	95.33
Average	98.54	94.42	94.17	94.26	94.28

Figure 9:

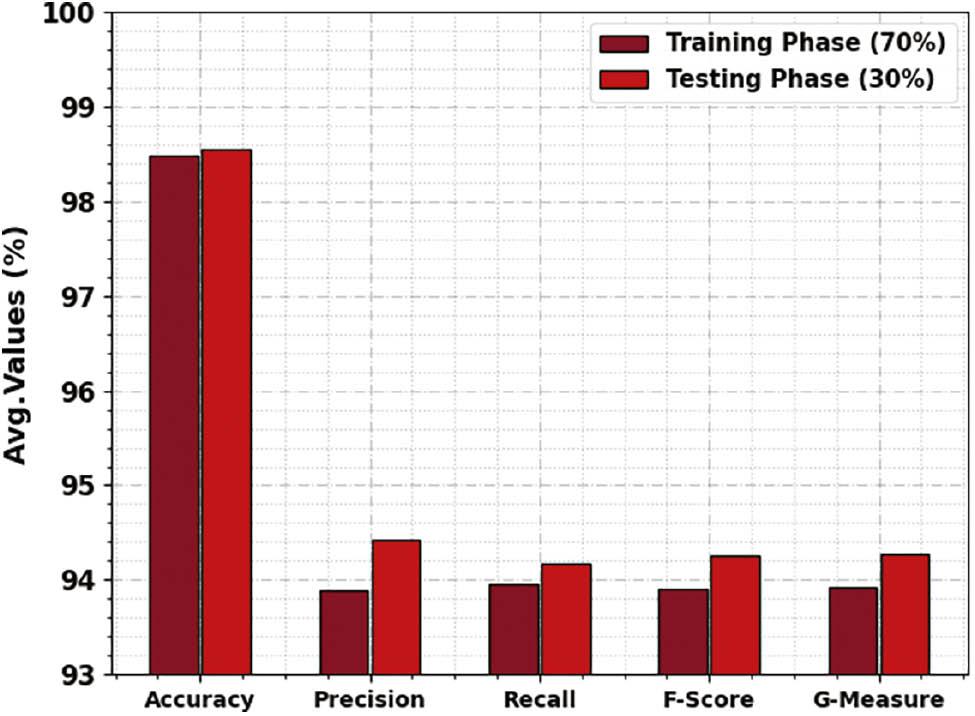
Average outcome of RGRC-GODSAE approach on 70:30 of TRP/TSP. Abbreviation: RGRC-GODSAE, robust gesture recognition and classification using growth optimizer with deep stacked autoencoder.

Figure 10 depicts the accuracy of the RGRC-GODSAE algorithm in the training and validation on 70:30 of TRP/TSP. The result portrays that the RGRC-GODSAE technique attains greater accuracy values over higher epochs. Furthermore, the greater validation accuracy over training accuracy specified that the RGRC-GODSAE method learns productively on 70:30 of TRP/TSP.

Figure 10:

Accuracy curve of RGRC-GODSAE method on 70:30 of TRP/TSP. Abbreviation: RGRC-GODSAE, robust gesture recognition and classification using growth optimizer with deep stacked autoencoder.

The loss analysis of the RGRC-GODSAE method in training and validation is given on 70:30 of TRP/TSP in Figure 11. The outcomes indicate that the RGRC-GODSAE method reaches a closer value of training and validation loss. The RGRC-GODSAE technique learns productively at 70:30 of TRP/TSP.

Figure 11:

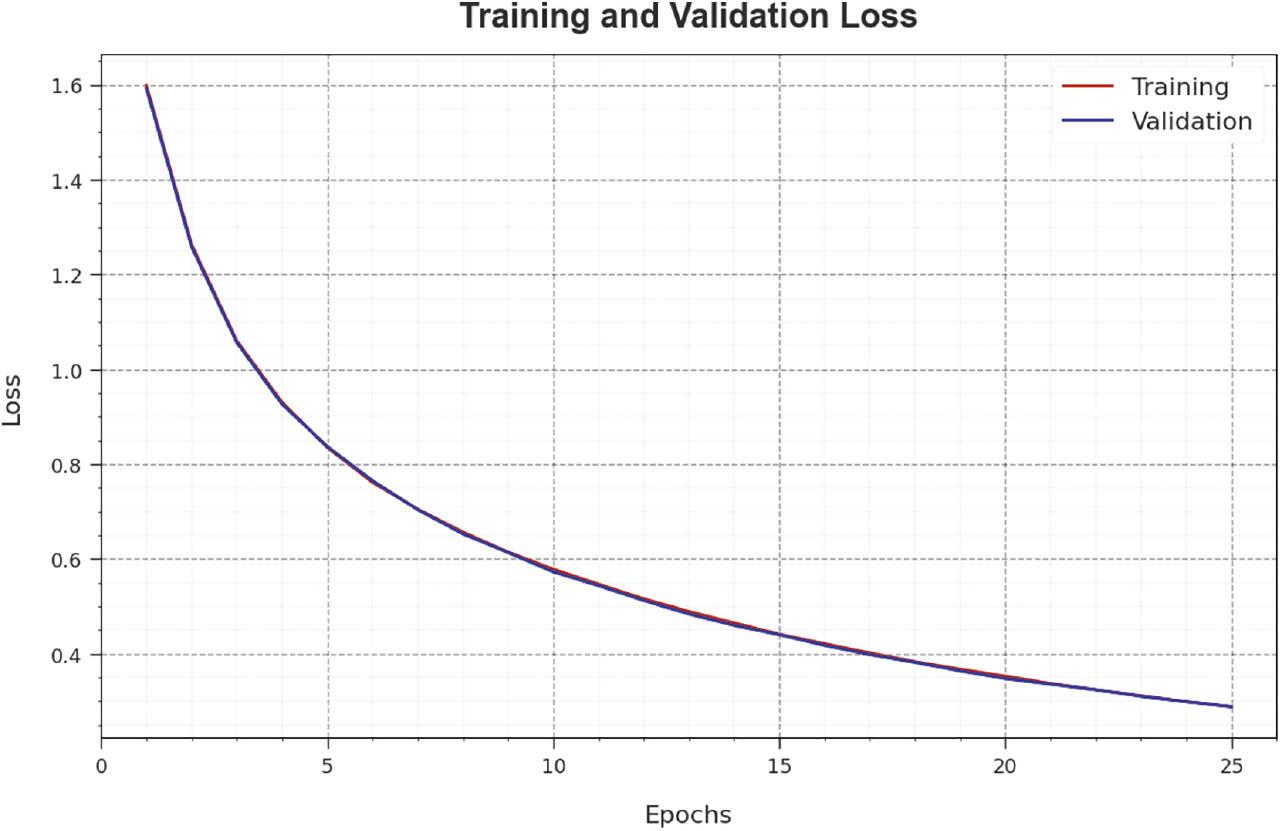
Loss curve of RGRC-GODSAE approach on 70:30 of TRP/TSP. Abbreviation: RGRC-GODSAE, robust gesture recognition and classification using growth optimizer with deep stacked autoencoder.

A brief PR curve of the RGRC-GODSAE technique is demonstrated on 70:30 of TRP/TSP in Figure 12. The figure states that the RGRC-GODSAE technique results in increasing values of PR. In addition, the RGRC-GODSAE technique can reach higher PR values in all classes.

Figure 12:

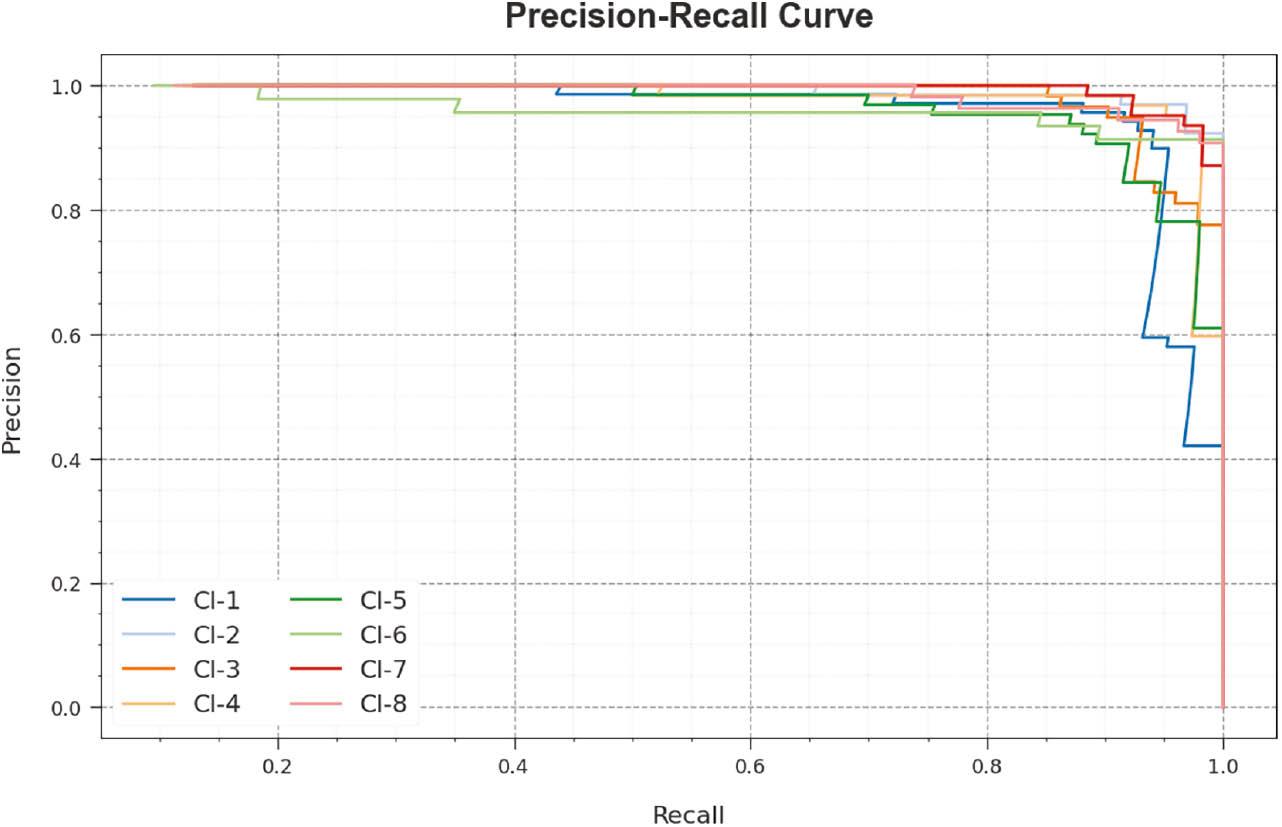
PR curve of RGRC-GODSAE approach on 70:30 of TRP/TSP. Abbreviations: PR, precision–recall; RGRC-­GODSAE, robust gesture recognition and classification using growth optimizer with deep stacked autoencoder.

In Figure 13, an ROC study of the RGRC-GODSAE technique is revealed at 70:30 of TRP/TSP. The figure describes that the RGRC-GODSAE approach resulted in improved ROC values. Besides, the RGRC-GODSAE algorithm can extend enhanced ROC values on all classes.

Figure 13:

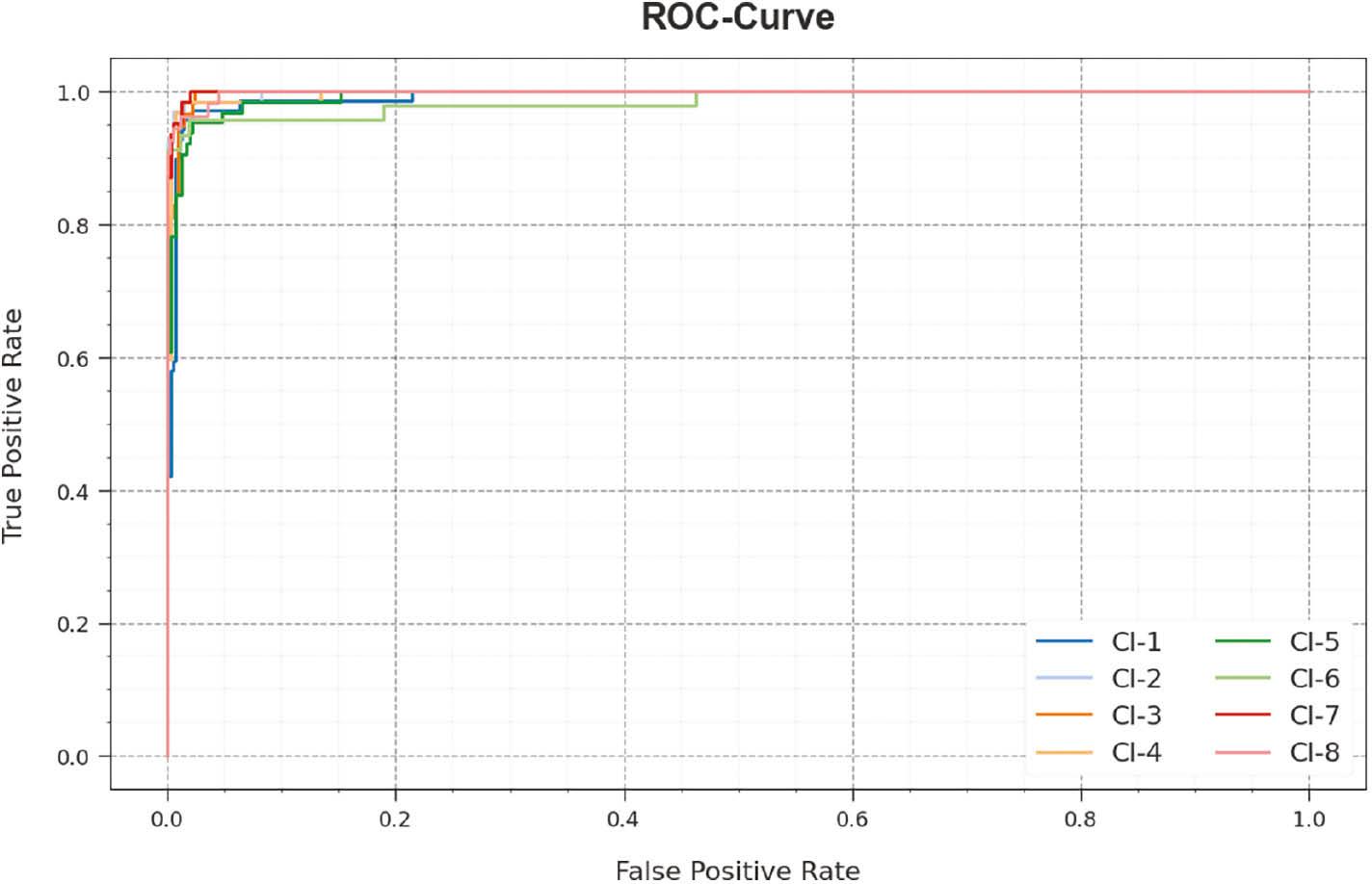
ROC curve of RGRC-GODSAE approach on 70:30 of TRP/TSP. Abbreviations: RGRC-GODSAE, robust gesture recognition and classification using growth optimizer with deep stacked autoencoder; ROC, receiver operating characteristic.

Finally, a comparison study of the RGRC-GODSAE technique with recent approaches in terms of different measures is given in Table 4 and Figure 14 ( Alduhayyem et al., 2023). The experimental values identified that the AlexNet, VGG-16, VGG-19, and GoogleNet models accomplish poor performance over other compared methods. At the same time, the YOLO-v3 model gains slightly enhanced results.

Figure 14:

Comparative outcome of RGRC-GODSAE algorithm with other methods. Abbreviation: RGRC-GODSAE, robust gesture recognition and classification using growth optimizer with deep stacked autoencoder.

Table 4:

Comparative outcome of RGRC-GODSAE algorithm with other methods.

Methods	Accuracy	Precision	Recall	F-Score
RGRC-GODSAE	99.77	99.08	99.06	99.07
TSOLWR-ODVIP	99.29	98.80	98.70	98.74
SSD-MobileNet	98.85	98.33	98.17	98.38
YOLO-V3	95.55	95.16	95.77	95.80
AlexNet	85.89	86.54	84.81	89.53
VGG-16	86.50	85.70	87.92	89.11
VGG-19	84.43	84.06	87.33	87.22
GoogleNet	88.77	86.80	89.05	86.66

Along with that, the TSOLWR-ODVIP and SSD-MobileNet models achieve moderately improved performance. However, the RGRC-GODSAE technique reaches outperforming results with a maximum accu _y of 99.77%, prec _n of 99.08%, reca _l of 99.06%, and F _score of 99.07%. These results show the betterment of the RGRC-GODSAE technique over other current methods.

CONCLUSION

In this study, we have introduced a new RGRC-GODSAE technique for effectual recognition and classification of gestures to aid visually impaired persons. The main aim of the RGRC-GODSAE technique lies in the accurate recognition and classification of gestures to assist visually impaired persons. The RGRC-GODSAE technique comprises several subprocesses, namely, GF-based noise elimination, ShuffleNet feature extractor, GO-based hyperparameter tuning, and DSAE-based gesture recognition. The design of the GO algorithm helps in optimal selection of the hyperparameters related to the ShuffleNet model. The experimental outcomes of the RGRC-GODSAE method take place on the benchmark dataset. The extensive comparison study showed the better gesture recognition performance of the RGRC-GODSAE technique over other DL models. In future, the gesture recognition rate of the RGRC-GODSAE technique can be boosted by advanced DL ensemble classifiers.

CONFLICTS OF INTEREST

The authors declare no conflicts of interest in association with the present study.

DATA AVAILABILITY STATEMENT

Data sharing does not apply to this article as no datasets were generated during the current study.

REFERENCES

1. Alduhayyem M, Alnfiai MM, Almalki N, Al-Wesabi FN, Hilal AM, Hamza M. 2023. Iot-driven optimal lightweight retinanet-based object detection for visually impaired people. Comput. Syst. Sci. Eng. Vol. 46(1):475–489

2. Chen Z, Liu X, Kojima M, Huang Q, Arai T. 2021. A wearable navigation device for visually impaired people based on the real-time semantic visual SLAM system. Sensors. Vol. 21(4):1536

3. De Fazio R, Mastronardi VM, Petruzzi M, De Vittorio M, Visconti P. 2022. Human–machine interaction through advanced haptic sensors: a piezoelectric sensory glove with edge machine learning for gesture and object recognition. Future Internet. Vol. 15(1):14

4. Fatani A, Dahou A, Abd Elaziz M, Al-qaness MA, Lu S, Alfadhli SA, et al.. 2023. Enhancing intrusion detection systems for IoT and cloud environments using a growth optimizer algorithm and conventional neural networks. Sensors. Vol. 23(9):4430

5. Fu Y, Lu Y, Ni R. 2023. Chinese lip-reading research based on ShuffleNet and CBAM. Appl. Sci. Vol. 13(2):1106

6. Gaidhani MR, Pagariya MP, Patil MA, Phad MT. 2022. Sign language recognition using machine learningInternational Conference on Innovative Computing, Intelligent Communication and Smart Electrical Systems (ICSES); Chennai, India. p. 1–5. [Cross Ref]

7. Hegde P, Devathraj N, Sushma SK, Aishwarya P. 2021. Smart glasses for visually disabled person. Int. J. Res. Eng. Sci. Vol. 9(7):62–68

8. Hegde R, Chitrashree RM, Dimple N, Shet HG, Deekshitha J, Soumyasri SM. 2022. Smart translation for physically challenged people using machine learning2022 IEEE International Conference on Data Science and Information System (ICDSIS); IEEE. p. 1–5

9. Jyothsna K, Kumar VM, Shambharkar S, Reddy DA, Bhoyar CN, Somkunwar RK. 2022. Face recognition automated system for visually impaired peoples using machine learning2022 International Conference on Data Science, Agents & Artificial Intelligence (ICDSAAI); Vol. Vol. 1. IEEE. p. 1–7

10. Lee ET, Fan Z, Sencer B. 2023. A new approach to detect surface defects from 3D point cloud data with surface normal Gabor filter (SNGF). J. Manuf. Process. Vol. 92:196–205

11. Miah ASM, Hasan MAM, Shin J, Okuyama Y, Tomioka Y. 2023. Multistage spatial attention-based neural network for hand gesture recognition. Computers. Vol. 12(1):13

12. Montazerin M, Zabihi S, Rahimian E, Mohammadi A, Naderkhani F. 2022. ViT-HGR: vision transformer-based hand gesture recognition from high density surface EMG signals2022 44th Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC); IEEE. p. 5115–5119

13. Muneeb M, Rustam H, Jalal A. 2023. Automate appliances via gestures recognition for elderly living assistance2023 4th International Conference on Advancements in Computational Sciences (ICACS); IEEE. p. 1–6

14. Padmavathi R. 2021. Expressive and deployable hand gesture recognition for sign way of communication for visually impaired people.

15. Raja SKS, Vivekanandan M, Kiruthika SU, Ayshwarya SARJ. 2019. Design and implementation of facial recognition system for visually impaired using image processing. Int. J. Recent Technol. Eng. Vol. 8(4):4803–4807

16. Rashid SMU, Ishar KNA, Sayed S. 2022. COMPANION-An Application for Impaired Persons. IJIRE. Vol. 3(2)

17. Samee NA, Atteia G, Alkanhel R, Alhussan AA, AlEisa HN. 2022. Hybrid feature reduction using PCC-stacked autoencoders for gold/oil prices forecasting under COVID-19 pandemic. Electronics. Vol. 11(7):991

18. Shen S, Wang X, Wu M, Gu K, Chen X, Geng X. 2023. ICA-CNN: gesture recognition using CNN with improved channel attention mechanism and multi-modal signals. IEEE Sens. J. Vol. 23(4):4052–4059

19. Shokat S, Riaz R, Rizvi SS, Khan I, Paul A. 2021. Detection of touchscreen-based Urdu Braille characters using machine learning techniques. Mob. Inf. Syst. Vol. 2021:1–16

20. Subburaj S, Yeh CH, Patel B, Huang TH, Hung WS, Chang CY, et al.. 2023. K-mer-based human gesture recognition (KHGR) using curved piezoelectric sensor. Electronics. Vol. 12(1):210

21. Xu C, Wu X, Wang M, Qiu F, Liu Y, Ren J. 2023. Improving dynamic gesture recognition in untrimmed videos by an online lightweight framework and a new gesture dataset ZJUGesture. Neurocomputing. Vol. 523:58–68

22. Yoo M, Na Y, Song H, Kim G, Yun J, Kim S, et al.. 2022. Motion estimation and hand gesture recognition-based human–UAV interaction approach in real time. Sensors. Vol. 22(7):2513

23. Zakariah M, Alotaibi YA, Koundal D, Guo Y, Mamun Elahi M. 2022. Sign language recognition for Arabic alphabets using transfer learning technique. Comput. Intell. Neurosci. Vol. 2022:4567989