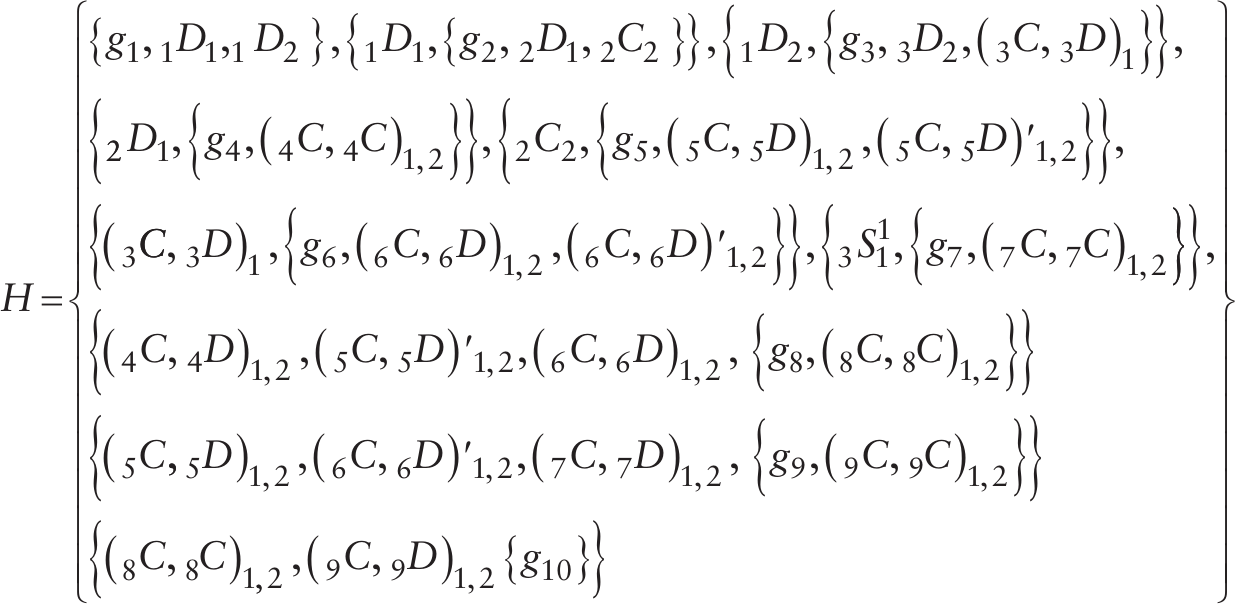Game Theory and a New Insight into How the Cuban Missile Crisis Was Resolved

Abstract

The purpose of this article is to investigate the Cuban Missile Crisis with new approaches. For this purpose, we analyse this crisis in two static and dynamic approaches. In the static approach, we look at the crisis through the perspective of credible threats. In the dynamic approach, the crisis is modelled using several game theoretic models. The models allow us to analyse the interplay of the capabilities and the feasibility objectives of each player after a conflict with the other player’s objectives and capabilities. The dynamic system of games has significant implications as an important insight for modelling strategic interactions in which players pursue goals for increasing their personal interests. Our findings give insight into how the two countries reached a compromise in the Cuban Missile Crisis.

Main article text

Introduction

Game theory provides the theoretical underpinnings of analytical techniques and their application in social research. Indeed, many fields of science have benefited from game theoretic models (Askari et al. 2019; Rapoport et al. 1976). Dynamic games provide a framework for modelling the behaviour of players in situations where there are dynamic strategic interactions (Ungureanu 2017; Yeung and Petrosian 2017). Robinson and Goforth (2005) and Van Long (2011) provide surveys of models of dynamic games in industrial organisation. In the Theory of Games and Economic Behavior, Morgenstern and Von Neumann write: “We repeat most emphatically that our theory is thoroughly static. A dynamic theory would unquestionably be more complete and therefore preferable” (1953: 44). Eshaghi and Askari recently introduced a new method of modelling in game theory, named the dynamic system of strategic games (Eshaghi and Askari 2018).

In a dynamic system of strategic games, such as the game maker game and the strategy-maker game, the pair of rational actions and new properties of games are presented, and with the help of these properties, the dynamics of players’ behaviours are studied. According to this feature, strategic games were divided into two classes, strategy maker games and games that were not strategy maker. Also, both strategy maker games and games that were not strategy maker were themselves divided into two groups. In this article, we present the required concepts and terms, outline some advantages of this modelling, and prove two propositions. Here, we consider strategic 2 × 2 games with perfect information. If a game produces other games, it is called a game maker game. In general, if the games $g_1^{’},g_2^{’},\dots ,g_n^{’}$ generate games $g_1^{’},g_2^{’},\dots ,g_n^{’}$ then g_i and $g_i^{’}$ are called producer and produced, respectively. In the dynamic system of games after the choice of strategy or rational action pairs is made by the players by entering into the new games, the productive game is out of reach. Therefore, the producer games are out of reach of the players, and they can influence the selection of strategies and games in the future only as a history of the system. (For more details about the dynamic system of games, refer to Eshaghi and Askari 2018; Eshaghi et al. 2019; Asghari et al. 2021; Babaei and Gordji 2022.)

As an application of the dynamic system of strategic games, we model the conflict between the Soviet Union and America after the Second World War to October 28, 1962. The Cold War was a state of geopolitical tension after the Second World War between powers in the Eastern Bloc and powers in the Western Bloc. Prior to 1957, Cuba had for many years been under the complete economic and political control of the United States. In late 1956 a revolution to overthrow the Batista regime was initiated by Fidel Castro, which triumphed in 1959. The situation was made more unstable by the unsuccessful US-sponsored Bay of Pigs invasion and a declaration by the Soviet Union of its willingness to aid Cuba in defending itself against the US (Fraser and Hipel 1982; Zagare 2014). Countries like the Soviet Union and the US also belong to different models of international relations and political systems. For modelling the Cuban Missile Crisis, we divide the period into five smaller periods, and in each of those periods we examine static games with perfect information.

The outline of the article is as follows: in section 2, we introduce the Threat game and credible and non-credible threats. In section 3, we model the conflict between the Soviet Union and the US after the Second World War to October 28, 1962. Section 5 concludes.

Credible and non-credible threats

The recently introduced static Threat game is an extension of the Chicken game (Askari et al. 2020). The Threat game has a Nash equilibrium of pure strategy, while the Chicken game has two equilibria with pure strategy. This new game includes three strategies F, T, and TF. In the Threat game, strategy F means any driver doesn’t use the brakes on the route and uses the only steering wheel to pull over, which is an invalid threat (because by holding the steering wheel, the player can swerve to the right or left before the crash). Strategy T means that the player doesn’t use the steering wheel on the route and uses only the brakes to stay on the route, and this is a threat-deterrent (because by using the brakes, the player can stay on the road and not deviate from the path, and the other player must either use the brakes or deviate from the path to avoid an accident or continue on her/his path and lead to an accident). Strategy TF means that the player doesn’t use the steering wheel and brakes on the route and only goes straight, and this is a strictly credible strategy.The Chicken game does not have a dominant strategy, but the Threat game has a dominant strategy.

Using the new game, the threats were divided into three categories. The first category includes non-credible threats. The term non-credible threat refers to the fact that even if one of the players has threatened the opposite party to use a specific strategy, if there is then a situation where he is forced to put his threat into action, being rational he will not execute the threat (Bolt and Houba 2006; Sun and Sun 2018; Zegart 2020). Threats which are not credible are not worth mentioning because the opposite party does not take them seriously, and therefore they will not have any affect on the change of the opponent’s strategy in the game. The second category includes credible-deterrent threats to deter and prevent struggles, in which a player threatens the opponents to select a strategy in order to warn the opponent, and the opponent believes the player possesses the ability to execute the threat. This is exactly the concept ordinary people apply to nuclear weapons. The weapons are not for attacking, but for deterrence. The third category includes a strictly-credible threat aiming to destroy the opponent, in which case the player has the necessary and sufficient motivation to carry out a threat even if the situation leads to a struggle.

Since the occurrence of this event 60 years ago, the Cuban Missile Crisis is a case which has been highly important in international affairs, and decision-making theorists and game theorists have made several efforts to analyse it. Well-known theorists such as Schelling, Fraser and Hipel, and Zagari have modelled the Cuban Missile Crisis (Fraser and Hipel 1982; Schelling 1980; Zagare 2014). By analysing the crisis using the Meta-game theory, Howard concluded that the two parties involved in the crisis reached a compromise (Howard 1971). Brams proposed a dynamic modelling framework called Theory of Moves to model this crisis (Brams 1944).

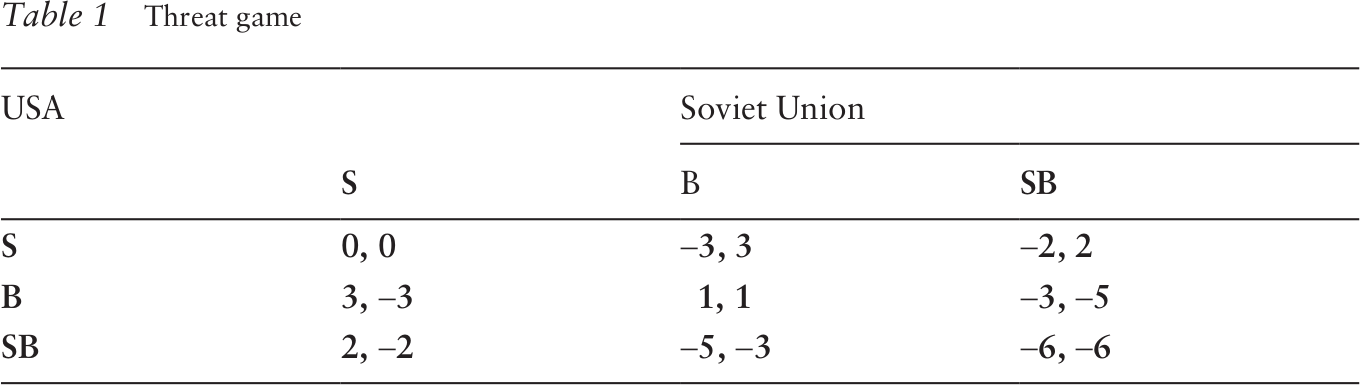
Here, using the Threat game, we analyse the Cuban Missile Crisis (see Table 1). Conceptually we start the analysis from when the US noticed the construction of missile sites in Cuba. In this game, the US had three strategies: forcing the Soviet Union to eliminate its missiles through mass media (S), blockade Cuba and seek a solution through diplomatic channels (B), and attacking Cuba (SB). The Soviet Union had three strategies: announcing that it sought to intensify the hostilities (S), keeping the missiles there and searching for a solution through diplomatic channels (B), or attacking the US (SB).

Table 1

Threat game

In this game, iterated elimination of strictly dominated strategies allows us to solve the game. For both players, SB is strictly dominated by (B). By eliminating this strategy, players have two strategies, S and B. Now for both players, S is strictly dominated by B. So the game equilibrium is (B.B), that is, the two countries use a credible-deterrent strategy to prevent an atomic war. In other words, the blockade of Cuba by the US and keeping the missiles there by the Soviet Union, along with the use of a diplomatic channel, was the same as engaging a brake against atomic war by both players. Therefore, this static analysis gives a logical insight as to why the two countries reached a compromise in the Cuban Missile Crisis.

Analysis of the Cuban Missile Crisis with a dynamic approach

The Soviet Union and US relations after the Second World War were sometimes strained. But the most important and dangerous crisis in the Soviet Union and US relations, which put the world on the edge of a devastating war, followed the establishment of Soviet missile bases in Cuba. The Soviet Union wanted to establish a massive arsenal of heavy weapons there in order to become the largest military station in the Caribbean. But Khrushchev’s trick was ultimately revealed. In October 1962 a US spy plane discovered a missile launch site to the west of Havana, which confirmed the establishment of medium-range missiles in Cuba (May and Zelikow 2002). To confront the danger of that threat to US security, the president convoked a war council, and for one week a serious and secret discussion was held in the White House. In this council, different suggestions were proposed, including bombing the missile launch platform, or an all-out military attack on Cuba and military occupation of the country. On 22 October 1962 Kennedy then informed the American people that the Soviet government had established missile bases in Cuba, a distance of one hundred miles from American beaches, and warned them that this presented a threat to the country’s security. In the same announcement he told the Soviet government that it must remove its missile bases from Cuba. Following this, he issued an order for a naval blockade of Cuba to prevent the transfer of the Soviet’s new missile equipment to Cuba (Kennedy 1969). This issue became a world crisis for one week. (For more information about the Cuban Missile Crisis, see Blaschke 2016; Crall and Martin 2013; and Gibson 2012.)

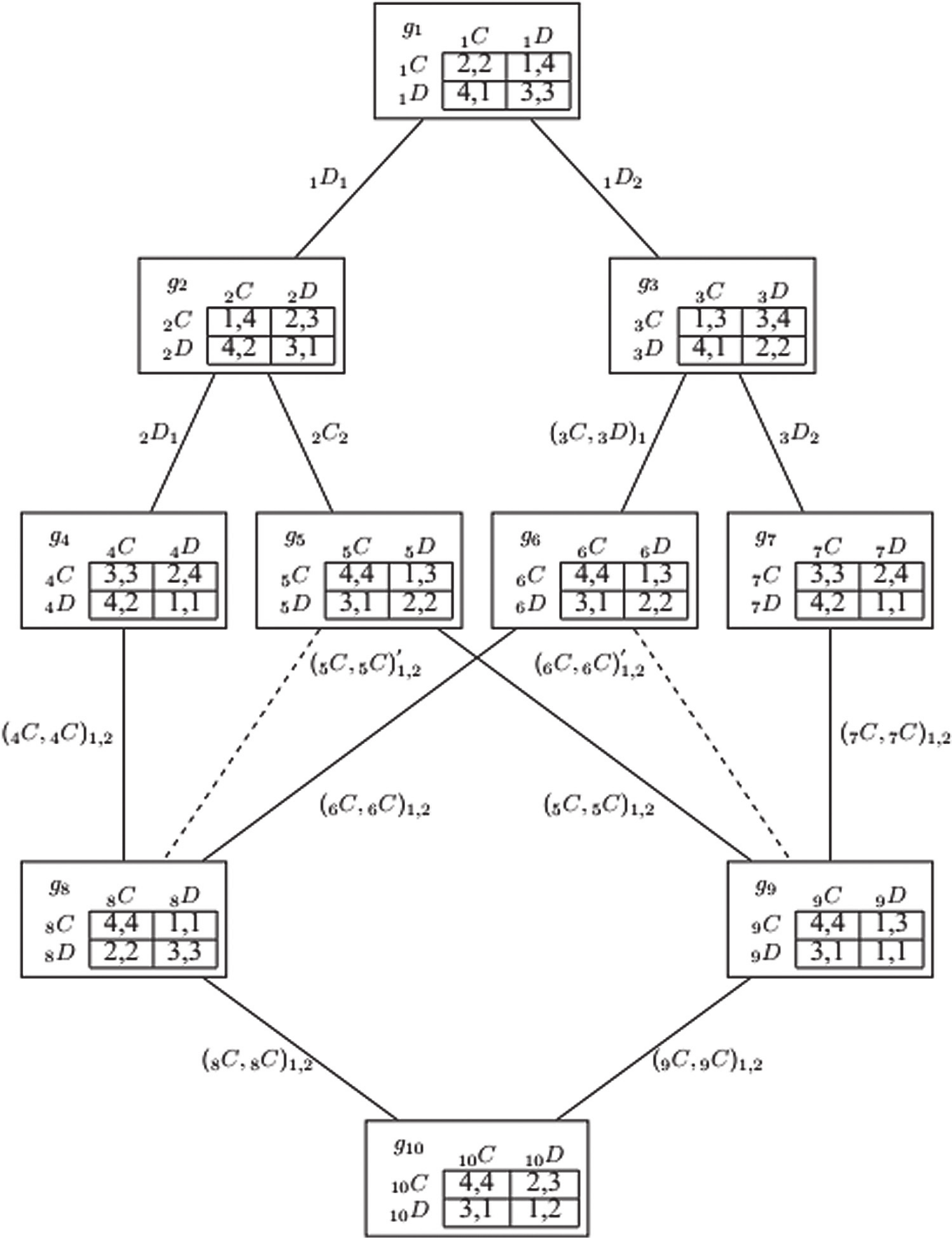
In this section, we propose a different model from the static one-play interaction of the Soviet Union and the US in in the Cuban Missile Crisis. Now we will use a dynamic system of games to model the relations between the Soviet Union and the US after the Second World War leading up to October 28, 1962. To this end, we divide the period into five smaller periods, and in each of those periods we examine static games with perfect information. The first period is from the end of the Second World War to October 13, 1962, which is represented by game g₁. The second period from October 14 to 22 is represented by games g₂ and g₃. The third period is from October 23 to 25 and is represented by games g₄, g₅, g₆ and g₇. The fourth period is from October 26 to 27 and is represented by games g₈ and g₉. And finally, the day of October 28 is represented by game g₁₀.

Relations between the Soviet Union and the US after the Second World War and during the 1950s constituted a Deadlock game in which they manifested minimal desire to cooperate with each other. As a result, both countries selected the non-cooperation strategy. The Deadlock game g₁ is shown in Figure 1. The row player (player 1) is the Soviet Union and the column player (player 2) is the US. The players’ set of actions include cooperation ₁C and defect ₁D. Players’ preferences in this node are the same order preferences of strategic game g₁. The game’s Nash equilibrium is (₁D,₁D). In g₁, dominant action ₁D₁ is defect and dominated action ₁C₁ is cooperation for player 1. Also, this game has a dominant action of defect ₁D₂ and dominated action of cooperation ₁C₂ for player 2. In other words, game g₁ is an action maker of order (2, 2). The only pair of rational actions for the players is (₁D,₁D)_1,2. Based on the players being rational, they select dominant action ₁D₁ and dominant action ₁D₂ for the continuation of the game. According to its dominant action, the Soviets were convinced in July 1962 to implement their Atomic Missile Establishment plan in Cuba in order to confront the US’s growing expansion.

Figure 1

Dynamic system of games between the Soviet Union and the US.

Action ₁D₁ leads to Hostage game g₂. The Soviet Union wanted to surprise the US. In this game, the Soviet Union has two possible actions: either cooperate ₂C through removing the missiles or defect ₂D and maintain the missiles. The US could reveal the issue ₂C or keep it secret ₂D . The game Nash equilibrium is (₂D,₂D) . This game has a dominant action of defect ₂D₁ and a dominated action of cooperation ₂C₁ for player 1. The dominant action ₂C₂ for player 2 is revealing the issue and the dominated action ₂D₂ is keeping it secret. The only pair of rational actions for both players is (₂D,₂C)_1,2.

Action ₁D₂ leads to the Self-Serving game g₃. In g₃ the US has two actions: either it cooperates ₃C by doing nothing or it defects ₃D through a blockade of Cuba. The Soviet Union also has two actions: either it cooperates ₃C to remove missiles through the diplomatic channel or it defects ₃D and maintains the missiles. The game Nash equilibrium is (₃C,₃D). Game g₃ is action maker of order (2, 1). This game has a dominant action of defect ₃D_1,2 and a dominated action of cooperation ₃C_1,2 for player 2. Pairs of rational actions for the players are (₃C,₃D)_1,2 and (₃D,₃D)₁.

Action ₂D₁ leads to the Chicken game g₄. In g₄ the Soviet Union has two possible actions: either it does not attack the US ₄C or it attacks the US ₄D. The US has two possible actions: either it does not attack the Soviet Union ₄C or it attacks the Soviet Union for retaliation ₄D. The game Nash equilibria are (₄C,₄D) and (₄D,₄C). Game g₄ is action maker of order (2, 0). In other words, this game is not action maker for the players. The players’ pairs of rational actions are (₄C,₄C)_1,2, (₄D,₄C)₁ and (₄C,₄D)₂.

Action ₂C₂ leads to the Stag Hunt game g₅. In g₅ the US has two possible actions: either through diplomacy it seeks a solution ₅C or through diplomacy it puts pressure on the Soviet Union ₅D. The Soviet Union has two possible actions: either it seeks a solution ₅C through diplomacy or it thinks about crisis intensification ₅D. The game Nash equilibria are (₅C, ₅C) and (₅D, ₅D). Game g₅ is action maker of order (2, 0). The players’ pair of rational actions are (₅C, ₅C)_1,2 and (₅D, ₅D)_1,2.

The pair of rational actions (₃C, ₃D)₁ leads to another Stag Hunt game g₆. In g₆ the Soviet Union has two possible actions: either it does not break the blockade ₆C or it breaks the blockade ₆D. The US has two possible actions: either it does not have a conflict ₆C with the Soviet ships or it has a conflict with the Soviet ships ₆D. The game Nash equilibria are (₆C, ₆C) and (₆D, ₆D). Game g₆ is action maker of order (2, 0). The players’ pair of rational actions are (₆C, ₆C)_1,2 and (₆D, ₆D)_1,2.

Action ₃D₂ leads to Chicken game g₇. In g₇ the US has two possible actions: either it does not attack the Soviet Union ₇C or it attacks the Soviet Union ₇D. The Soviet Union has two possible actions: either it does not attack the US ₇C or it attacks the US in a retaliatory invasion ₇D. The game Nash equilibria are (₇C, ₇D) and (₇D,₇C). Game g₇ is action maker of order (2, 0). The players’ pairs of rational actions are (₇C, ₇C)_1,2, (₇D, ₇C)₁ and (₇C, ₇D)₂.

Based on players’ rationality and strategic preferences, players selecting pairs of rational actions (₄C, ₄C)_1,2, (₅C, ₅C)_1,2 and (₆C, ₆C)_1,2 move to Coordination game g₈. In g₈ the Soviet Union has two possible actions: either it issues the command for its ships not to move toward Cuba ₈C or it thinks about resolving the crisis through negotiation ₈D. The US has two possible actions: either it issues the command that its ships not confront the Soviet ships ₈C or it thinks about resolving the crisis through negotiation ₈D. The game Nash equilibria are (₈C, ₈C) and (₈D, ₈D). Game g₈ is action maker of order (2, 0). The players’ pairs of rational actions are (₈C, ₈C)_1,2 and (₈D, ₈D)_1,2.

Based on players’ rationality and strategic preferences, players selecting pairs of rational actions (₅C, ₅C)_1,2, (₆C, ₆C)_1,2 and (₇C, ₇C)_1,2 move to game g₉. In g₉ the Soviet Union has two possible actions: either it removes the missiles from Cuba ₉C or it maintains the missiles in Cuba ₉D. The US has two possible actions: either it removes its blockade of Cuba ₉C or maintains its blockade of Cuba ₉D. The game Nash equilibria are (₉C, ₉C) and (₉D, ₉D). Game g₉ is action maker of order (2, 2). In g₉ the weak dominant action ₉C₁ for the Soviet Union is removing the missiles and its weakly dominated action ₉D₁ is maintaining the missiles. For the US the weakly dominant action ₉C₂ is removing its blockade and the weakly dominated action ₉D₂ is maintaining its blockade. The players’ pairs of rational actions are (₉C, ₉C)_1,2, (₉D, ₉D)_1,2, (₉D, ₉C)₁ and (₉C, ₉D)₂.

Based on players’ rationality and strategic preferences, players selecting pairs of rational actions (₈C, ₈C)_1,2 and (₉C, ₉C)_1,2 move to Win-Win game g₁₀. In this game both players have two possible actions, cooperation ₁₀C and defection ₁₀D. The game Nash equilibrium is (₁₀C, ₁₀C). With this the players have no desire to continue and so this completes the system.

The dynamic system of games with strategic games between the Soviet Union and the US is represented by the graph in Figure 1. The history of the system is as follows.

In Figure 1, if the Chicken game had a dominant action even for one player, an atomic war would probably have occurred. This weakness of not having the dominant action in this game causes the players to consider their strategic preferences and not to use tactical preferences inside the game. In other words, players prefer strategic preferences over tactical preferences. Recognising this is important for understanding why the two countries reached a compromise in the Cuban Missile Crisis.

Conclusion

A dynamic system of games helps us to analyse an event by dividing it into different periods and dynamically using several games. This enables the event analyst to evaluate the decisions and strategies that the players have chosen in order to achieve a reasonable and acceptable result. The system also shows the impact of players’ decisions on each other, and the impact of the results from one period on the results of subsequent periods.

In this study, we used a dynamic system of strategic games to investigate the interaction between the Soviet Union and the US from the end of the Second World War until October 28, 1962, that is, up to the end of the Cuban Missile Crisis. A dynamic system of games is a combination of dynamic and static interactive situations that are moving forward. In our case we divided the full time interval into five periods, and in each period we reviewed static games with complete information. Each country, based on its forces and capabilities, sought to achieve its goals and objectives in Cuba. The result of the dynamic game was that the countries reached a compromise, as in fact occurred in history. Looking at the strategies adopted in each period, we can see what sorts of strategies have the potential to achieve such a compromise. Thinking about other cases of conflict beyond the case we examined, this study shows how a dynamic system of strategic games can provide a frame for analysing what sorts of cooperative behaviours among players can potentially yield an exit from the conflict.

Notes

1.

Somayeh Shaabani is a PhD Candidate and teaching assistant in the Faculty of Mathematics, Statistics and Computer Science at Semnan University in Semnan, Iran. Madjid Eshaghi Gordji is a Professor of Mathematics at Semnan University in Semnan, Iran.

References

1. N. AsghariM. Eshaghi GordjiA. Ghaffari (2021) “Modelling US-China relationship: a game theory perspective”. International Journal of Nonlinear Analysis and Applications 12(2): 1371–82.

2. G. AskariM. Eshaghi GordjiC. Park (2019) “The behavioral model and game theory”. Palgrave Communication 5(57): 1–8.

3. G. AskariM. Eshaghi GordjiS. ShabaniJ.A. Filipe (2020) “Game theory and trade tensions between advanced economies”. European Research Studies Journal, 23 (Special issue 1): 50–65.

4. S. BabaeiM. Eshaghi Gordji (2022) “Modeling political and economic relations between Norway and Russia: A behavioral game theory approach”. The Pure and Applied Mathematics 29(2): 141–60.

5. Anne M. Blaschke (2016) “Running the Cold War: gender, race, and track in cultural diplomacy, 1955–1975”. Diplomatic History 40(5): 826–44.

6. Wilko BoltHarold Houba (2006) Credible Threats in Negotiations: A Game-Theoretic Approach. Cham: Springer Science & Business Media.

7. S.J. Brams (1944) Theory of Moves. Cambridge: Cambridge University Press.

8. Dennis A. CrallThomas M. Martin (2013) “Cool hand nuke: lessons from the quiet diplomacy of the Cienfuegos non-crisis”. Foreign Policy Analysis 9(2): 189–201.

9. M. Eshaghi GordjiG. Askari (2018) “Dynamic system of strategic games”. International Journal of Nonlinear Analysis and Applications, 9(1): 83–98.

10. M. Eshaghi GordjiN. AsghariM. De la Sen (2019) “Modeling political and economic relations between Russia and Turkey: a game theory approach”. International Journal of Computer Science and Network Security 19(2): 163.

11. Niall M. FraserKeith W. Hipel (1982) “Dynamic modelling of the Cuban missile crisis”. Conflict Management and Peace Science 6(2): 1–18.

12. David R. Gibson (2012) Talk at the Brink: Deliberation and Decision during the Cuban Missile Crisis. Princeton, NJ: Princeton University Press.

13. Nigel Howard (1971) Paradoxes of Rationality: Games, Metagames, and Political Behavior. Cambridge, MA: MIT Press.

14. Robert F. Kennedy (1969) 13 Days: The Cuban Missile Crisis October 1962. New York: W. W. Norton & Company.

15. Ernest R. MayPhilip Zelikow (eds) (2002) The Kennedy Tapes: Inside the White House during the Cuban Missile Crisis. New York: W. W. Norton & Company.

16. Oskar MorgensternJohn Von Neumann (1953) Theory of Games and Economic Behavior. Princeton, NJ: Princeton University Press.

17. A. RapoportM. GuyerG. Gordon (1976) The 2 × 2 Games. Ann Arbor: Michigan University Press.

18. David RobinsonDavid Goforth (2005) The Topology of the 2 x 2 Games: A New Periodic Table. Vol. 3. New York: Psychology Press.

19. Thomas C. Schelling (1980) The Strategy of Conflict. Cambridge, MA: Harvard University Press.

20. Shaorong SunNa Sun (2018) “Credible commitment and credible threat in games”, in S. SunN. Sun, Management Game Theory. Singapore: Springer, 63–7.

21. Sergiu Ungureanu (2017) “Dynamic contracting under permanent and transitory private information”. International Journal of Game Theory 46(3): 667–92.

22. Ngo Van Long (2011) “Dynamic games in the economics of natural resources: a survey”. Dynamic Games and Applications 1(1): 115–48.

23. David YeungOvanes Petrosian (2017) “Infinite horizon dynamic games: a new approach via information updating”. International Game Theory Review 19(04): 1–23.

24. Frank C. Zagare (2014) “A game-theoretic history of the Cuban Missile Crisis”. Economies 2(1): 20–44.

25. Amy Zegart (2020) “Cheap fights, credible threats: the future of armed drones and coercion”. Journal of Strategic Studies 43(1): 6–46.