1. INTRODUCTION
Nanomachines are heralded as the next revolution in science [1, 2], but even revolutions have to start simple. One of the simplest possible nanomachine is a cilium: a long “hair,” fixed at one end, and driven by motor units into a beating motion at the other end. Natural motile cilia typically have transport functions. Artificial cilia are already used for the same purposes, to transport fluids in lab-on-a-chip applications and for self-propelled nanoswimmers [3]. Natural cilia are large, complex assemblies of multiple parts with different functions. Taken to the extreme, however, a cilium could even be built as a single, comparatively small molecule.
Despite the simplicity of the cilium concept, several design challenges have to be met, also for a molecular-sized cilium, if it is to be used for transport: (1) One single cilium entity is useless to produce significant transport. Therefore, the cilia have to be mass-produced. (2) Transport is only meaningful relative to another nonmoving entity, and it has to happen at an interface. Hence, the cilia have to be mounted on a surface. (3) At the surface, they should stand upright rather than lie down. (4) Randomly scattered arrangements on a surface will likely hamper the transport function; it should rather be a well-controlled mass-arrangement. (5) The motor unit of the cilium only has to generate a bending motion, which appears to be simple. However, useful transport is unidirectional; therefore, the bending should happen in only one direction.
Aim (1) is easy to achieve for a molecular cilium, since traditional chemical synthesis always produces astronomically many molecules. Aims (2), (3), and (4) have been achieved by the platform concept [4, 5]: The cilium is mounted in perpendicular fashion on a triazatriangulenium (TATA) platform. Without and with cilia attached, the TATA units form well-ordered arrangements on various surfaces, with the spacings between the TATA units being controllable via substituents on their periphery.
A simple motor unit for a cilium is the well-established azobenzene or its improved derivative diazocine [6, 7, 8]. Both undergo trans → cis isomerization upon excitation with light of suitable wavelengths, and can be switched back in similar fashion, in preparation for the next stroke. However, even if one of these molecules were aligned into an ideal angular orientation, its trans → cis bending can still happen in two different, opposite directions. That is, no solution to problem (5) has been found so far.
To remedy this situation, Tellkamp et al. [9] have proposed a new molecular design (cf. Figure 1): One or two additional five-membered rings are annealed to diazocine, with the intention to sterically allow isomerization only in one of the two possible directions. These compounds, indandiazocine (ID) and diindandiazocine (DID), have already been synthesized and mounted to a TATA platform [9]. However, experimental and/or theoretical investigations of their photodynamics are still lacking.
Here we provide first theoretical simulations of ID and DID, in order to uncover their photodynamical pathways, the typical timings needed for photoisomerization, and the quantum yields to be expected. In particular, we test if the new feature, unidirectionality of photoswitching, is indeed realized. All of these investigations are done in direct comparison to our earlier work on the parent compound diazocine [6, 7, 8]. In a forthcoming article [10], we will describe simulations of ID and DID used as motor units in artificial molecular cilia.
ID and DID are distinguished by (1) their respective E and Z isomers (E-ID, Z-ID, E-DID, Z-DID) and (2) for DID also by their stereo information, i.e. its meso or racemic form (DIDmeso, DIDrac; cf. Figures 1 and 2). All of these forms were included in the present work.
The remaining text is structured as follows: First we will summarize the computational details for the static and dynamic calculations in Section 2. To benchmark the results and our computational method of choice, we also performed ab initio calculations for the ground-state structures. These will be presented Section 3, followed by the main results of the present investigations: the simulated UV and CD spectra (Section 4) and the excited-state dynamics (Section 5).
2. COMPUTATIONAL DETAILS
For geometry optimizations of ID, DIDrac, and DIDmeso structures and molecular dynamics (MD) simulations, we used the semiempirical AM1 method [11], which was reparametrized against theoretical and experimental data of azobenzene [12] and was coupled with a floating-occupation configuration-interaction (FOCI) ansatz by Granucci et al. [13]. In previous work [6, 8], we have explicitly verified that this approach yields good agreement with results from experiment and from higher level theoretical treatments, for the closely related compound diazocine. Therefore, it can be expected to be of similar quality for the present compounds. Nevertheless, we supply further benchmark results in Sections 3 and 4. For the CI part, 94 selected determinants were used as in the reparametrization process [12]. The MD simulations also included the quantum decoherence correction of Granucci et al. [14] with a (non-optimized) σ-value of 0.1 a.u. and all other needed parameters set to the default values.
The following procedure was performed for all compounds: For the ground-state MD simulations, one 15 ps long trajectory including Brownian motion at 298.15 K was run. From this trajectory, the starting structures for 200 fewest-switching surface-hopping trajectories [15] starting on the first excited state (S1) were sampled. These excited-state trajectories were propagated for 2.5 ps. The time step for all trajectories was set to 0.1 fs.
For benchmarking purposes, the semiempirical results were compared against ab initio data: the optimized FOCI-AM1 structures were re-optimized with the second-order Møller–Plesset perturbation theory (MP2) method and Dunning's correlation-consistent triple-zeta basis set (cc-pVTZ) [16], the excitation energies and CD spectra from the RI-MP2/cc-pVTZ optimized structures were calculated using the second-order approximate coupled cluster (CC2) method and the same basis set. The MP2 and CC2 calculations were used with the resolution of identity (RI) technique [17, 18, 19, 20, 21] and the frozen core approximation. The MP2 und CC2 calculations were done with the Turbomole (version 6.5) program [22]. The semiempirical calculations were performed with the MOPAC 2002 [23] program package, which was modified and extended by Granucci et al. [12, 13] to include direct classical–mechanical dynamics.
3. GEOMETRY OPTIMIZATION
The optimized FOCI-AM1 structures are shown in Figure 2. To assess the similarity of all re-optimized ab initio structures with their semiempirical counterparts, the root mean square deviation (RMSD) value was calculated using visual molecular dynamics (VMD) [24] after structural alignment (Table 1).
| Z | E | |
|---|---|---|
| ID | 0.26 | 0.28 |
| DIDrac | 0.69 | 0.32 |
| DIDmeso | 0.29 | 0.46 |
The RMSD values show an overall good agreement between the semiempirical and ab initio optimized structures. To further investigate the similarity, selected degrees of freedom (DOF) of the structures were chosen for comparison.
These DOFs are the CNNC and CCCC (ethylene bridge atoms) dihedral angles and, to see how much the structures are bent in the Z form, the distance of the two carbon atoms of the benzene rings in para position (CpCp, in reference to the azo unit) (Table 2).
| FOCI-AM1 | RI-MP2 | |||||
|---|---|---|---|---|---|---|
| CNNC/° | CCCC/° | CpCp/Å | CNNC/° | CCCC/° | CpCp/Å | |
| Z-ID | –2.4 | –31.7 | 6.2 | –1.9 | –37.5 | 5.8 |
| Z-DIDrac | 6.2 | 82.5 | 7.8 | 6.0 | 74.4 | 7.2 |
| Z-DIDmeso | 7.1 | 28.8 | 6.5 | 8.7 | 40.3 | 6.2 |
| E-ID | 137.9 | 93.9 | 8.3 | 147.6 | 92.7 | 8.4 |
| E-DIDrac | 137.1 | 86.0 | 8.2 | 146.6 | 84.2 | 8.3 |
| E-DIDmeso | 134.5 | 51.7 | 7.9 | 147.2 | 51.7 | 8.2 |
While the CNNC dihedral angles for the Z isomers show good agreement between the two methods, the CCCC dihedral differs by 6–12°. It is not clear whether this causes or is caused by the opening of the molecule indicated by the longer distance between the para carbon atoms of the rings. The connection between these two DOFs can be seen when looking at the corresponding values of the E isomers. There, the CCCC dihedral and CpCp distance is nearly identical for the FOCI-AM1 and RI-MP2 optimized structures.
For the CNNC dihedral, we find slight differences of about 10°. This might be due to the fact that the AM1 method used here was reparametrized for azobenzene, which is planar with a dihedral angle of 180° in the Z form. This clearly is not the case for the compounds studied here, which is why the results had to be checked against appropriate ab initio calculations. This discrepancy will be discussed in more detail in the following section.
Table 3 shows the energy differences for the FOCI-AM1 and RI-MP2 optimized isomer pairs, where we also see good agreement between the results of the two methods, with differences of 4–6 kcal/mol. The small energy difference between the DIDrac isomers might be due to the fact that except for the CNNC dihedral the molecular frame is nearly identical (RMSD = 0.61 Å). For the other isomers we find less similarity: RMSD(DIDmeso) = 0.78 Å, RMSD(ID) = 1.60 Å. However, none of the discrepancies mentioned in this subsection are large enough to invalidate the FOCI-AM1 approach for the present purposes.
4. UV AND CD SPECTRA
The FOCI-AM1 UV spectra were calculated from the ground-state trajectory by binning the vertical excitation energies for every structure during the run. The results are shown in comparison to the experimental data [25] in Figure 3.
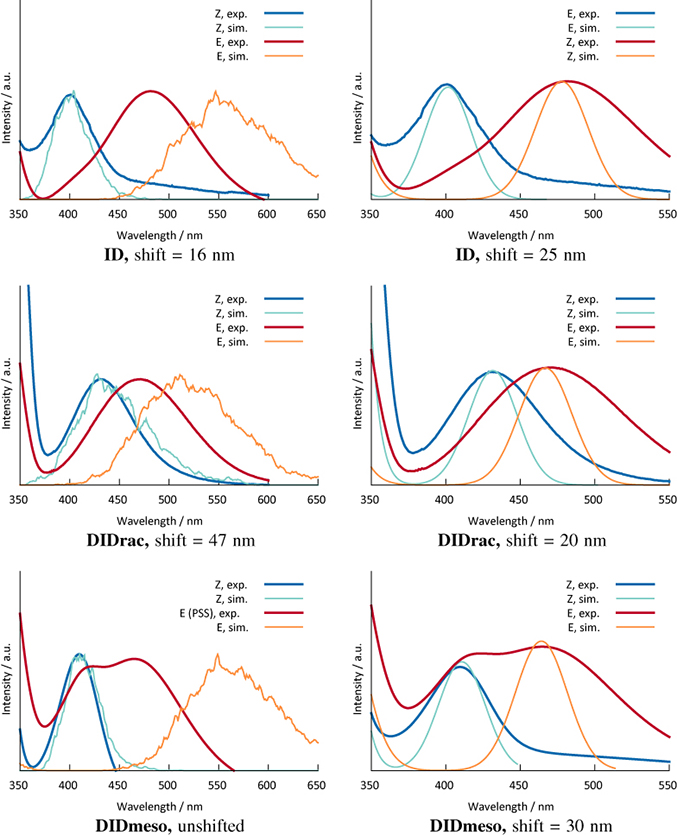
A comparison of all experimental and calculated vertical excitation energies is shown in Table 4.
| exp. | FOCI-AM1a | RI-CC2 | exp. | FOCI-AM1a | RI-CC2 | |
|---|---|---|---|---|---|---|
| Z-ID | 401 | 417 ± 19 | 377 | 280 | 274 ± 8 | 274 |
| Z-DIDrac | 431 | 488 ± 26 | 412 | 314 | 276 ± 8 | 290 |
| Z-DIDmeso | 409 | 413 ± 18 | 381 | 303 | 270 ± 7 | 279 |
| E-ID | 481 | 572 ± 36 | 453 | 307 ± 10 | 296 | |
| E-DIDrac | 471 | 562 ± 34 | 447 | 289 | 300 ± 9 | 295 |
| E-DIDmeso | 464 | 562 ± 34 | 434 | 313 ± 10 | 299 | |
All values in nanometer.
The deviations are the standard deviations from the average vertical excitation value of the ground-state trajectory after thermal equilibration.
In the RI-CC2 data in Table 4, we see a constant shift of 20–30 nm with regard to the experimental values for the excitation for every isomer pair, while the excitation is reproduced a bit better. The resulting spectra in Figure 3 were prepared by convoluting the line spectra of Table 4.
The FOCI-AM1 differences to the experiment are the result of parametrization against azobenzene, which was addressed before and was also seen in the theoretical work of Carstensen et al. for the parent system [6]. One explanation why this effect can be seen drastically for the E isomers is the twisted CNNC dihedral, which is planar for E-azobenzene. The twisting may lead to a non-optimal orbital overlap affecting the π and π* orbitals of this DOF, which would then lead to an energy shift for the excitations from the n-orbitals of the nitrogen atoms, where the twist effect presumably is smaller or absent.
This explanation would also hold true for the Z-ID and Z-DIDmeso structures, where we find smaller differences to the experiment, since the dihedral angle does not differ much from the one in Z-azobenzene and thus has the same electronic features. The excitation energy played an important role in the reparametrization process of the AM1 method [12]. For the Z-DIDrac structure we see the same large shift from the experimental excitation energy, also resulting from the structural difference to the Z-form of azobenzene.
To our experience with direct photodynamics simulations based on semiempirical CI approaches in the past 10 years, these discrepancies are not serious enough to cause concerns about the applicability of the methods used here.
Regarding the photochemical properties of the studied compounds, we see a good separation of the bands of 60–80 nm in the experiment, which allows to address the E and Z isomers separately, which was correctly predicted by the RI-CC2 excitation energies.
The five-membered rings as new features of ID and DID not only provide the desired steric constraints but also impose chirality on these molecules. In fact, they probably are the smallest chiral photoswitches currently known. Chiral compounds can be characterized by their CD spectra. Figure 4 shows our simulated CD spectra for both isomers of ID and DIDrac, as a further point of direct contact between simulation and experiment. Since the shifting problem from above still applies here, we will only compare the general features of the results for the ID and DIDrac compounds, for which the experimental data are available [25] (Figure 5). While the calculated (relative) intensities do not fit the experimental result well (which is not to be expected at this level of theory and for systems where the chirality centers are not part of the chromophore [26]), the overall shape, which is dictated by the sign of the intensities, does fit the experiment.

5. EXCITED-STATE DYNAMICS
The excited-state dynamics were calculated to validate the claim that all compounds perform a unidirectional movement upon irradiation, while also yielding information about the quantum yields and time scales. After careful evaluation of all 400 trajectories for each compound, we find that the molecules indeed only perform the desired unidirectional movement. For this we checked the time progression for the CNNC dihedral angle, for which we find an opening or closing, respectively, in only one direction, i.e. Z isomers starting from about 0° always open up to 140° instead of –140°, in contrast to what was found for the parent system brAB [8]. Figure 6 shows this for all compounds and isomers, where all CNNC and CCCC dihedrals were averaged over all reactive trajectories.

The central CCCC dihedral, i.e. the atoms of the ethylene bridge that are also present in the parent system, was examined as a rather basic comparison of the reaction mechanism. For brAB, it is now established [6, 8, 27, 28, 29] that the reaction starting from the Z isomer is not finished when the CNNC dihedral reaches the value it has in the E product. After that stage, the CCCC dihedral still needs considerable time (several 100 fs) to also reach the conformation in the E-form, which for the Z → E reaction is the rate-determining step. This problem is absent in the DID compound, where we find similar CCCC conformations in both E and Z forms. In the dynamics, we see this in the oscillation of the dihedral angle around its initial value throughout the propagation. The Z-ID structures, which are more brAB-like, still show the opening of the CCCC dihedral, but here it happens on the same time scale as the CNNC opening, because of the strain coming from the extra five-membered rings.
Results for the quantum yields are shown in Table 5. They document an overall good agreement to the experimental [7] and theoretical [8] quantum yields obtained for the parent compound (brAB) in solution, but deviate from our previous gas phase values for the same compound [6]. Since our calculations were performed in the gas phase, these findings need to be discussed: in his theoretical work, Carstensen [8] found that there is actually a huge effect on the quantum yields and dynamical behavior coming from the solvent, which qualitatively changes the theoretical results from the previous gas phase calculations [6] to agree better with the experimental values (Table 5). Since we do not have any experimental quantum yields for the three compounds studied in this work, we have to compare them with the results from the parent system, which qualitatively fit well even though we neglect the solvent. Further pieces for this puzzle are provided in the following paragraphs.
The population inversion (PI) time, i.e. the time when 50% of the trajectories return to the ground state (), is a good indicator for an ultrafast reaction. Both DID isomer pairs return between 50 and 100 fs to the ground state where they finally isomerize to the E or Z isomer, respectively (Table 6).
The PI time for all E → Z reactions are about the same among each other, but also in comparison to the gas phase brAB results in Ref. [6]. The reason for this can be seen in the E-forms of the ID and DID structures, which do not differ much electronically and in terms of important DOFs (see Table 2), so that the initial conditions for the trajectories are about the same and ultimately lead to comparable behaviors during the dynamics. For the Z → E isomerization process we see that the inversion times for the compounds studied in this work are at least two times higher than the PI time for the parent compound in the gas phase [6]. For the reaction starting from Z-ID we see a factor 5 in comparison to Z-brAB and even to the Z-DID compounds a factor of 2–3. The reason for this can also be found in the ground-state structures, where we see the following trend: From Z-ID to Z-DIDmeso to Z-DIDrac we see an opening of the CNNC dihedral, which makes the structures more “E-like,” and thus makes them reach the coupling region, i.e. the conical intersection, much faster during the MD simulation. This finding can be compared to the work of Carstensen [8], where he has seen a pre-orientation effect for the Z isomer resulting from the solvent. So with the added five-membered rings in the ID and DID molecules this intermolecular steric effect appears at the intramolecular level. Figure 7 shows the steric effect resulting from the H atoms, which are extending in-between the phenyl rings causing them to open. In Z-ID only one H atom can be found between the rings, which is why we see more Z-brAB-like behavior for this structure. In the Z-DIDmeso structure we find two H-atom opposing each other, causing a more open form. Finally, in the Z-DIDrac structure, there are three H-atoms pointing between the rings, which leads to a noticeable steric effect resulting in a very open CNNC dihedral.

This might explain why we get similar results for the mechanism, quantum yields and PI times as the QM/MM study, although we are neglecting solvent molecules in this work. Another (but less important) reason for the Z-ID → E-ID population process being that much slower than for the parent system might be the quantum decoherence correction, which was not available in the work of Carstensen et al. [6, 8].
Table 7 shows the averaged values for important DOFs and their change over time during the excited-state dynamics in the same fashion as Table V in Ref. [8] for easier comparison with the values of brAB. With these we can show the following: (1) The values of the three DOFs at the starting point of the trajectories do not differ much, therefore one cannot argue that the sampling of starting structures biases the calculated quantum yields. (2) The same holds true for the final values just before the transition to the S0 surface, where we only find marginal differences, with the exception of the CNNC dihedral angle of ID during Z → E isomerization. (3) The only noticeable effect on the outcome of the trajectory comes from the change of the CNNC dihedral angle over time (dCNNC/dt) just before the surface-hop, which is (in absolute values) much higher for trajectories that will reach the product form and could imply a steeper gradient near the conical intersection being an important factor for the reactivity. (4) Neither of the values concerning the CCCC dihedral in Table 7 shows an effect on the reactivity, because there are only small differences between reactive and unreactive trajectories, which was also the case for the parent system [8], though. Therefore this is another piece of evidence that only the steric effect from the added five-membered rings (which are not present in brAB) is the cause for the CCCC dihedral no longer playing a role during the isomerization process. We also note that Table 7 is biased against early surface-hops to S0 that usually result in a trajectory hopping back to S1 in less than ~10 fs, which can also be seen as the kinks in the population plots of the E → Z reactions (Figure 8) for all isomers before 50 fs. This is an artifact of the surface-hopping approach and could possibly be fixed with an optimized σ-value for the quantum decoherence correction. However, since there does not seem to be a noticeable effect on the dynamics, this is a minor problem, because the trajectories usually return to the S1 in less than ~10 fs so that no significant geometrical changes can happen during this time. Therefore only the value for the first hop to S0 in Table 7 should be affected by this, which can be seen when comparing this value to the PI time.
| ID | DIDrac | DIDmeso | ||||
|---|---|---|---|---|---|---|
| Reactive | Unreactive | Reactive | Unreactive | Reactive | Unreactive | |
| Z → E | ||||||
| First hop to S0/fs | 151.16 | 153.34 | 57.99 | 57.99 | 96.06 | 93.52 |
| CNNC (init.)a/° | –2.17 | –1.89 | 4.09 | 5.41 | 5.83 | 6.62 |
| CCCC (init.)a/° | –29.51 | –30.49 | 81.01 | 80.95 | 26.22 | 29.04 |
| CNNC (final)b/° | –61.40 | –33.41 | 74.66 | 82.19 | 84.64 | 84.74 |
| CCCC (final)b/° | –45.44 | –43.16 | 85.52 | 85.57 | 36.77 | 37.97 |
| dCNNC/dtb/° fs–1 | –0.90 | –0.28 | 0.98 | –0.77 | 1.21 | 0.30 |
| dCCCC/dtb/° fs–1 | –0.07 | –0.08 | 0.13 | 0.21 | 0.19 | 0.27E |
| E → Z | ||||||
| First hop to S0/fs | 26.44 | 32.59 | 36.13 | 45.61 | 27.52 | 42.10 |
| CNNC (init.)a/° | 138.02 | 137.84 | 137.03 | 137.10 | 135.43 | 135.97 |
| CCCC (init.)a/° | 90.76 | 91.59 | 84.22 | 83.81 | 46.81 | 45.84 |
| CNNC (final)b/° | 101.71 | 99.61 | 97.66 | 98.14 | 102.30 | 98.57 |
| CCCC (final)b/° | 93.55 | 93.82 | 86.05 | 87.27 | 48.38 | 47.63 |
| dCNNC/dtb/° fs–1 | –2.46 | –1.49 | –1.74 | –1.32 | –2.62 | –0.72 |
| dCCCC/dtb/° fs–1 | 0.44 | 0.33 | 0.39 | 0.31 | 0.34 | 0.18 |
All values are averaged over the respective number of reactive and unreactive trajectories. The change of the DOF (dX/dt) was calculated from the last three frames before the surface-hop to S0.
aValues for the initial geometry, i.e. at the Franck–Condon point; bValues for the last geometry on the S1 surface, right before the surface-hop.

6. CONCLUSIONS
In this work we investigated different novel photoswitches based on diazocine and their dynamic behavior upon photoexcitation. The main purpose was to find out if the claim of an unidirectional switching process can be validated. Note that presence or absence of this feature is a gross qualitative decision that does not hinge upon smallness of quantitative deviations. Thus, our results definitely prove this novel behavior of ID and DID, after examination of 200 trajectories per compound and their isomers.
Although we saw defects of the FOCI-AM1 method in the UV spectra, which are an artifact of the reparametrization of the method, previous works on the dynamics of diazocine [6, 8] showed good agreement with experimental findings. For benchmarking purposes of the FOCI-AM1 semiempirical method, we compared to ab initio results for the ground-state structures and the vertical excitation energies, using the RI-MP2 and RI-CC2 methods, respectively. We found good agreement between the FOCI-AM1 and RI-MP2 structures, but some discrepancies for the FOCI-AM1 excitation energies and RI-CC2 energies, which show an excellent agreement to the experimental results. Nevertheless, we can still expect the FOCI-AM1 photodynamics simulations to provide a qualitatively correct picture.
The results from the excited-state dynamics – quantum yields and PI times – demonstrate that ID and DID have ultrafast photo-deexcitation dynamics, qualitatively similar to their parent compound brAB. Quantitative inspection of quantum yields and PI times, however, exhibits significant differences. In effect, the gas phase photodynamics of ID and DID appear to be similar to the photodynamics of brAB in solution. This can be explained by the additional five-membered rings providing steric and dynamic effects on the photodynamics that are very similar to those of surrounding solvent molecules.
Taken together, these findings support the expectation that (di)indandiazocines will turn out to be an important contribution to the toolbox of molecular motor units. They inherit robust, ultrafast photodynamics and further superior photophysical properties from their parent compound diazocine, and add the property of unidirectional motion, which is vital for many nano-engineering applications. In a forthcoming publication [10], we will exploit this new feature, with simulations of fully fledged, artificial molecular cilia, using these compounds as motor units.



